Ich versuche die im Titel stehende Behauptung mit Induktion zu beweisen, scheitere aber beim Induktionsschritt und sehe noch nicht so sehr, wie ich meine Voraussetzung nutzen kann.
Das hatte ich bisher.
Beweis (durch vollständige Induktion).
Induktionsanfang. Sei n_0=2 und ein beliebiges Dreieck gegeben. Betrachte nun die längste Seite (die Grundseite) und fälle ein Lot auf diese Seite, sodass dieses durch den zur Grundseite gegenüberliegenden Eckpunkt verläuft. Damit hat man zwei neue rechtwinklige Dreiecke erhalten, womit die Aussage für n=2 wahr ist.
Induktionsvoraussetzung. Es sei nun ein beliebiges Dreieck gegeben, was in n ≥ 2 rechtwinklige Dreiecke zerlegt ist, wobei n ≥ 2 beliebig, aber fest ist (IV).
Induktionsschritt. Dann kann auch ein beliebiges Dreieck in n+1 rechtwinklige Dreiecke zerlegt werden.
Meine Idee war nun, einfach ein neues beliebiges Dreieck zu betrachten, welches schon gerade das Dreieck aus meiner IV mit enthält und wo auch dort schon n Zerlegungen vorliegen. Das Problem ist aber, dass ich damit zwei neue rechtwenklige Dreiecke hätte (siehe Bild)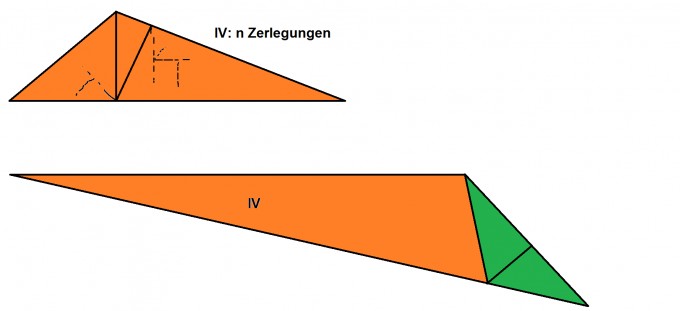
Wo liegt mein Denkfehler?