Aufgabe:
Sei D der Bereich, der von den Kurven
$$ C _ { 1 } ( t ) = ( 2 \pi - t + \sin ( t ) , 1 - \cos ( t ) ) ^ { \top } $$
und
$$ C _ { 2 } ( t ) = ( t , 0 ) ^ { \top } $$
mit \( t \in [ 0,2 \pi ] \) begrenzt wird. Bestimmen Sie \( s_2 \), wenn \( S = \left( s _ { 1 } , s _ { 2 } \right) ^ { \top } \in \mathbb { R } ^ { 2 } \) den Schwerpunkt von D bezeichnet, mit Hilfe des Satzes von Green in der Ebene. Gehen Sie wie folgt vor:
a) Stellen Sie \( s_2 \) in Form von Flächenintegralen dar.
b) Nutzen Sie den Satz von Green, um die Flächenintegrale zu berechnen.
Die Fläche um die es geht ist die Fläche zwischen der x-achse und c_1. c_2 stellt die Achse dar:
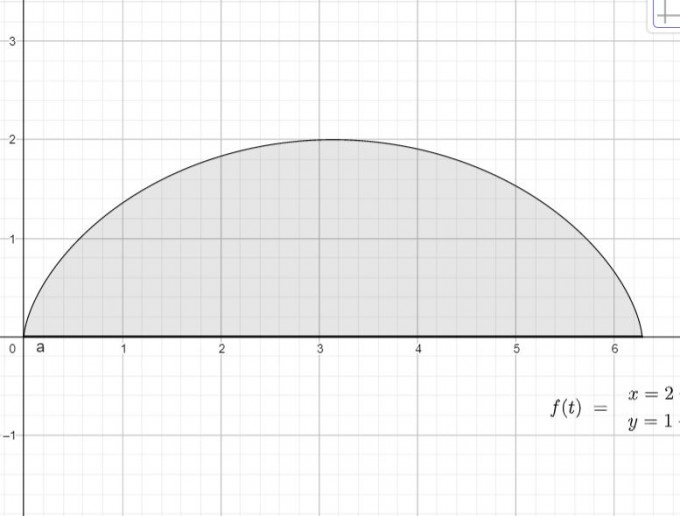
Ich glaube s_2 ist y_s des Schwerpunkts und das sollte man doch mit der folgenden Formel ausrechnen können:
$$y_{s} = \frac{\int_{a}^{b} \! f^{2} (x) \, dx }{2\int_{a}^{b} \! f(x) \, dx }$$
Wie aber stelle ich s_2 als Flächenintegral dar?
Wie wende ich den Satz von Green hier an?