Der Punkt \(Q\) soll also auf einer Geraden liegen, die durch \(S\) geht und parallel zu \(AB\) verläuft. Und der Winkel \(\angle BQS\) soll ein Rechter sein. Folglich steht eine Gerade durch \(BQ\) senkrecht auf \(SQ\) und somit auch senkrecht auf \(AB\). Da \(AB\) genau in Y-Richtung verläuft, muss \(Q\) dieselbe Y-Koordinate wie \(B\) haben. Und da alle Punkte auf der Geraden durch \(SQ\) konstante X- und Z-Koordinaten haben, kann man \(Q\) direkt hinschreiben: $$Q = \begin{pmatrix} s_x\\ b_y\\ s_z\end{pmatrix} = \begin{pmatrix} 0\\ 7\\ 6\end{pmatrix}$$ Falls sich Dein Lehrer mit dieser einfachen Antwort nicht zufrieden gibt und Du es 'ausrechnen' sollst, so geht das wie folgt: Du benötigst dazu die Kenntnis über die Normalform einer Ebene, musst wissen wie man eine Gerade im Raum aufstellt und wie man den Schnittpunkt von beiden berechnet.
\(Q\) erhält man als Schnittpunkt der Geraden (blau) durch \(S\), die parallel zu \(AB\) verläuft und der Ebene (grün), die \(B\) enthält und senkrecht auf \(AB\) steht.
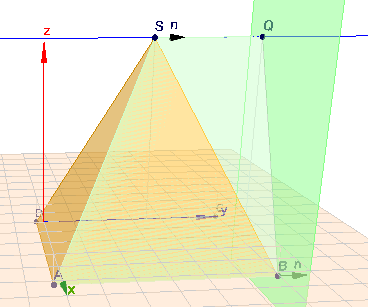
(Bem.: auch wenn es auf Grund der Zentralperspektive nicht so aussieht; \(E\) steht senkrecht auf der XY-Ebene)
Ein Vektor \(\vec{n}\) der in Richtung \(AB\) zeigt ist $$\vec{n} = f \cdot (B-A)$$ wobei \(f\) ein beliebiger Faktor ist. Es kommt hier nur auf die Richtung an. In diesem konkreten Fall wähle ich \(f=1/7\), dann bekommt man handliche Zahlen: $$\vec{n} = f \cdot (B-A) = \frac17 \left( \begin{pmatrix} 3\\ 7\\ -1\end{pmatrix} - \begin{pmatrix} 3\\ 0\\ -1\end{pmatrix}\right) = \begin{pmatrix} 0\\ 1\\ 0\end{pmatrix} $$ Damit steht die Gerade \(g\) durch \(S\) fest: $$g: \space \vec{x} = S + t \cdot \vec{n} = \begin{pmatrix} 0\\ 3,5\\ 6\end{pmatrix} + t \cdot \begin{pmatrix} 0\\ 1\\ 0\end{pmatrix}$$ Die Ebene \(E\) hat den gleichen Normalenvektor \(\vec{n}\) und enthält \(B\) also: $$\begin{aligned} E: \space \vec{n} \cdot \vec{x} &= \vec{n} \cdot B \\ \end{aligned}$$ Mit Einsetzen der Geraden erhält man das \(t_Q\) für den Schnittpunkt: $$\begin{aligned} \vec{n} \cdot (S + t_Q \cdot \vec{n}) &= \vec{n} \cdot B \\ \vec{n} \cdot S + t_Q \cdot \vec{n}^2 &= \vec{n} \cdot B \\ t_Q \cdot \vec{n}^2 &= \vec{n} \cdot B - \vec{n} \cdot S \\ t_Q &= \frac{\vec{n} \cdot B - \vec{n} \cdot S}{\vec{n}^2} \end{aligned}$$ Nun die Zahlen einsetzen $$ t_Q = \frac{1 \cdot 7- 1 \cdot 3,5}{1^2} = 3,5$$ \(t_Q\) in die Geradengleichung einsetzen liefert \(Q\) $$Q = S + t_Q \cdot \vec{n} = \begin{pmatrix} 0\\ 3,5\\ 6\end{pmatrix} + 3,5 \cdot \begin{pmatrix} 0\\ 1\\ 0\end{pmatrix} = \begin{pmatrix} 0\\ 7\\ 6\end{pmatrix}$$ Falls noch irgendwas nicht klar ist, so frage bitte nach.
Gruß Werner