Extremwertaufgaben : 1. Grundriss eines Hauses , Länge vom Flur bestimmen. 2. Zwei Kanäle...

Question

Aufgabe:

1) Der Grundriss eines Hauses zeigt drei Räume und einen Flur mit Breite x (siehe Skizze). Wie groß soll x gewählt werden, damit die Grundfläche der drei Räume möglichst groß ist, wobei der Umfang aller Wände insgesamt 90 m betragen soll.

(2) Zwei Kanäle mit Breite a = 1 m und b = 1, 5 m schneiden sich rechtwinklig (siehe nachstehende Abbildung). Wie lang darf ein Balken (dessen Dicke vernachlässigt werden kann) höchstens sein, damit er von einem Kanal in den anderen gebracht werden kann? Runden Sie bitte Ihr Ergebnis auf zwei Nachkommastellen auf und schreiben Sie bitte bei Ihren Berechnungen alle Ihre Schritte ausführlich auf, damit diese gewertet werden können. Weisen Sie bitte explizit nach, dass es sich bei der Lösung um eine Extremstelle handelt und geben Sie bitte explizit die Länge des Balkens an.

PS: Was ist genau mit Umfang aller Wände gemeint?

Comments

Vom Duplikat:

Titel: WIe groß ist x? und wie komme ich darauf?

Stichworte: maximum,textgleichung

Aufgabe

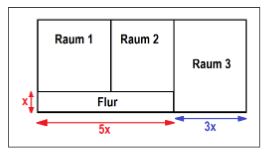
Der Grundriss eines Hauses zeigt drei Räume und einen Flur mit Breite x(sieheSkizze) .Wie groß soll x gewähl werden, damit die Grundäche der drei Räume möglichst groß ist, wo bei der Umfang aller Wände insgesamt 90m betragen soll.

Problem/Ansatz:

Wie gehe ich bei solchen AUfgaben vor? Da muss man doch irgendiwe mit dem Maximum rechnen,oder?
wenn es geht, das endergebnis, damit ich weiß, ob ich richtig gerechnet habe.

vielen dank schon mal

---

Umfang aller Wände insgesamt 90m betragen soll.

Gehe mit diesem Textteil zurück zum Fragesteller. Das ist so nicht eindeutig / unverständlich formuliert.

---

Vom Duplikat:

Titel: Flächeninhalt der Grundfläche der drei Räume zusammen möglichst groß wird?

Stichworte: raum,fläche,wand,extremwertaufgabe,flächeninhalt

Text erkannt:

Unten stehende Skizze zeigt den Grundriss eines Hauses, das aus drei Räumen und einem Flur der Breite x besteht. Die Gesamtlainge der Wände soll 90 m betragen.

Wie groß ist die Breite \( x \) zu wählen, damit der Flächeninhalt der Grundfläche der drei Räume
zusammen möglichst groß wird?
Legen Sie einen sinnvollen Definitionsbereich der Flächenfunktion bezüglich x fest.
Bearbeitungshinweise :
1) Notwendige und hinreichende Bedingung für das Maximum sind nachzuweisen
2) Das Endergebnis ist auf zwei Nachkommastellen zu runden
\begin{tabular}{|c|c|c|}
\hline Raum I & Raum 2 & Raum 3 \\
\hline\( x \) & Flur & \\
\hline \( 5 x \) & \( 3 x \) \\
\hline
\end{tabular}

Aufgabe:

Problem/Ansatz:

wie kann ich die Funktion wissen!

Answer 1

Hallo

 1) ich denke es meint die Summe  der Länge aller Wände, die auf dem Plan sichtbar sind.  Dadurch bekommt man eine Beziehung zwischen der Länge bzw. x und der unbekannten Breite b. Da auch in den Flächen b auftritt kann man es ersetzen .

2) berechne die Länge als Summe der 2 Längen in den 2 Kanälen, und benutze dazu den Winkel α   dann das max von L in Abhängigkeit von α

Gruß lul

Comments

dann das max von L

Du meinst hoffentlich das min von L

---

Hallo mir ist leider immer noch nicht klar was damit gemeint ist:

"1) ich denke es meint die Summe  der Länge aller Wände, die auf dem Plan sichtbar sind.  Dadurch bekommt man eine Beziehung zwischen der Länge bzw. x und der unbekannten Breite b. Da auch in den Flächen b auftritt kann man es ersetzen ."

---

nicht klar was damit gemeint ist

Sehr verständlich, denn man weiß wirklich nicht, ob mit "Wand" die zu mauernde oder die zu tapezierende Wand gemeint ist.

---

Tut mir leid, ich verstehe Sie immer noch nicht!

---

Stimmt es so? 8x + 8x + 3x + 4a = 90 

---

Der Umfang von von einem Rechteck ist doch 2*a+2*b

in diesem fall 2*8x+2*b

wie bekommt mann das den da raus

F(x)=8x(x+a)-5x2 und die Länge aller Wände (2) 90=19x+4a? könnte das einer erklären ?

---

Hallo

 es geht um die Räume, ohne Flur, da darfst du nicht die ganze Fläche des Rechtecks nehmen. die Breite ist a+x deshalb die Fläche des Hauses 8x*(x-a) davon abgezogen die Fläche des Flurs 5x*x.

die Wände musst du alle addieren: aussenrum 2*8x+2*(x+a) innen : 5x+(x+a)+a

Gruß lul

Answer 2

a sei die Länge der senkrechten Wand von Raum 1. Dann ist die Fläche aller Räume (1) F(x)=8x(x+a)-5x² und die Länge aller Wände (2) 90=19x+4a. Löse (2) nach a auf und setze in (1) ein. Dann das Übliche: Nullstelle der ersten Ableitung.

Comments

Fläche aller Räume (1) F(x)=8x(x-a)-5x2 und die Länge aller Wände (2) 90=19x+4a

Musst du wohl noch mal nachrechnen.

---

F(x) habe ich nachgebessert. Für die Verbesserung der anderen Gleichung bitte ich um einen Vorschlag.

Answer 3

Länge aller Wände:

4a+3x+10x+3x=90 daher a=22,5-4x.

Fläche der drei Räume:

F=a·5x+(a+x)·3x

a einsetzen:

F=(22,5-4x)·5x+(22,5-4x+x)·3x

Vereinfachen. Nullstelle der ersten Ableitung bestimmen. 

Answer 4

Die Fläche der 3 Räume ist:

A=5x(y-x)+3xy oder (1) A(x)=8xy-5x²

Die Länge aller Wände ist:

90=3y+(y-x)+8x+8x+5x=4y+20x oder (2) y=(90-20x)/4

(2) in (1) einsetzen:

A(x)=8x·(90-20x)/4-5x² oder A(x)=180x-35x². Das ist die Funktion.  

Comments

Das hast du hier doch schon nicht gekonnt.

---

Fehler gefunden. Wurde nachgebessert.

---

Achtung. Antwort wurde verändert.