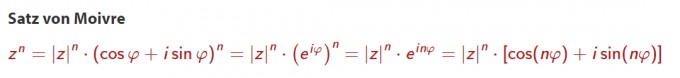Wichtiger Hinweis:
Wenn Moivre gefordert wird, mußt Du es auch danach berechnen,
ansonsten gib es Punktabzug .
für den Zähler ergibt sich:
a) Betrag berechnen |z|=√(1^2 +1^2)=√2
b)Winkel :tan(φ)= Imaginärteil/Realteil =1/1 ->φ= π/4 (1.Quadrant)
->(√2* e^((i π)/4))^8
=(√2)^8 * e^( 2*i π)
= 16 (cos(2π) +i sin(2π))
=16 *( 1 +i *0)
=16
das Ganze dann noch mit dem Nenner und dann zusammenfassen
Ergebnis Nenner: -8i
->= 16/(-8i)= 2i
algebraische Form : z= 0+2i