Geschwindigkeitsfunktion

Question

Aufgabe:

Zeit- Geschwindigkeitsfunktion v eines Körpers mit v(t)=-t^2+3*t+1

Problem/Ansatz:

Ermittle wann der Körper 20/3m zurückgelegt hat.

Also Integral(v(t)), dann habe ich die Wegfunktion. Das mit 20/3 gleichsetzen und die große Lösungsformel anwenden..richtig?

Answer 1

deine Ideen sind richtig, aber

\( s(t) = \int\limits_{0}^{t} (-x^2+3x+1) dx = -1/3 ·t^3 + 3/2·t^2 + t \)  

gibt die Entfernung vom Ausgangspunkt bei t=0 an, an dem sich der Körper zur Zeit t befindet. Da die Geschwindigkeit bei deiner Funktion auch negative Werte annimmt (Körper bewegt sich rückwärts!) kann die Entfernung 20/3 Meter auch mehrfach vorkommen.

Hier führt  die Gleichung  -1/3 t³ + 3/2 t² + t  = 20/3

       auf    t^3 - 9/2·t^2 - 3·t + 20 = 0

    [ eine der ganzzahligen Lösungen durch Probieren finden, Polynomdivision, pq-Formel                              oder Cardanoformeln ]

mit den Lösungen   t₁ = 5/2  ,   t₂ = 4  ,   [  t₃ = -2 entfällt ]

Eine genauere Betrachtung der Funktion ergibt den Teilgraph

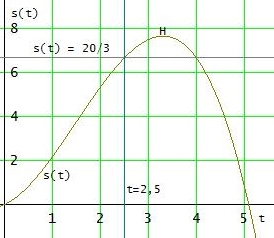
Der Körper hat die 20/3 m  nach t₁ = 2,5 s  zurückgelegt! 

Ab t_H  bewegt er sich rückwärts und erreicht die Entfernung 20/3 m vom Ausgangspunkt zur Zeit t₂ = 4s noch einmal :-)

Gruß Wolfgang

Comments

Ich denke die 4s entfallen auch

Ermittle wann der Körper 20/3m zurückgelegt hat.

vs.

Ermittle wann der Körper die 20/3m Marke erreicht.