Hallo Roland,
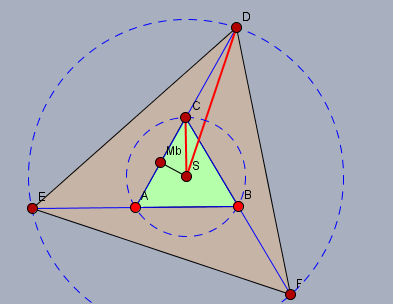
auf Grund der Drehsymmetrie fallen die Schwerpunkte beider Dreiecke im Punkt \(S\) zusammen. Das Verhältnis der beiden Flächen der Dreiecke \(\triangle ABC\) und \(\triangle DEF\) ist gleich dem Quadrat des Verhältnisses zweier korrespondierender Strecken. Demnach ist $$\frac{F_{DEF}}{F_{ABC}} = \frac{|SD|^2}{|SC|^2}$$ Sei \(|AB|=|CA|=s\), dann ist $$|SC| = \frac23 \cdot \frac12s\sqrt{3} = \frac s3 \sqrt{3}$$ und nach Pythagoras ist (wg. Höhe und Seitenhalbierende) $$ |SD|^2= |DM_b|^2 - |SM_b|^2 =\left( \frac 32 s\right)^2 - \left( \frac13 \cdot \frac12s \sqrt 3\right)^2 \\ \quad = \left( \frac 94 + \frac1{12} \right) s^2 = \frac{7}{3} s^2$$ Einsetzen in die Gleichung mit den Verhältnissen: $$\frac{F_{DEF}}{F_{ABC}} = \frac {\frac{7}{3} s^2}{\frac 13 s^2} = 7$$
Noch 'ne Lösung
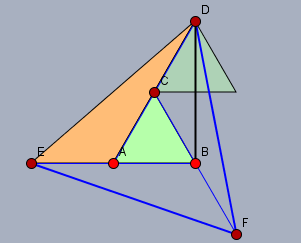
Die Höhe \(|BD|\) des Dreiecks \(\triangle EAD\) ist genau zweimal so groß, wie die Höhe des Dreiecks \(\triangle ABC\). Seine Grundseite \(|EA|\) ist gleich lang zur Grundseite \(|AB|\) des Dreiecks \(\triangle ABC\). Folglich ist der Flächeninhalt von \(\triangle EAD\) doppelt so groß wie vom \(\triangle ABC\). Da das Dreieck \(\triangle DEF\) aus drei Dreiecken der Größe \(\triangle EAD\) und aus einem Dreieck \(\triangle ABC\) besteht, ist sein Flächeninhalt $$F_{DEF} = 3\cdot(2F_{ABC}) + F_{ABC} = 7 F_{ABC}$$
Gruß Werner