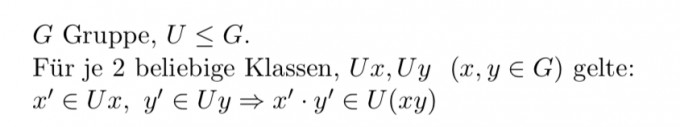U <= G heißt Normalteiler von G zeigen

Question

Aufgabe:

U ≤ G heißt Normalteiler von von G, wenn Ux = xU ∀x ∈ G, d.h. Links- und Rechtsnebenklassen von U sind identisch. Zeigen Sie: U Normalteiler von G ⇔ * ist wohldefiniert.

Zeigen Sie anhand davon, dass G abelsch ⇒ U Normalteiler von G.

Ansatz:

"⇒" : Seien ux, ux' ∈ Ux. z.z. uxux'∈ U_{x x'}

"⇐" : Satz(Anhang) z.z. Ux = xU

Comments

U Normalteiler von G ⇔ * ist wohldefiniert.

Was ist "*"?

Answer 1

G abelsch ⇒ U Normalteiler von G

Sei G abelsch. Für jedes x∈B gilt

    xU = {g ∈ G | ∃u∈U: g = xu}

       = {g ∈ G | ∃u∈U: g = ux} (weil G abelsch)

       = Ux.

Also ist U Normalteiler von G.