Hätte man das Ganze eigentlich auch mit Vektoren beweisen können?
Ja - das geht sogar ziemlich 'straight forward'. D.h. es ist eine ziemliche Rechnerei, aber eben "nur" eine Rechnerei. Im Gegensatz zum 'geometrischen' Beweis - wie in der Antwort von hj2166, der eine gewisse Kreativität erfordert!
Ich nenne \(\vec{AB} = a\) und \(\vec{AD} = b\). Der Vektor \(\vec{BN} = \tau b\) mit \(\tau \in \mathbb{R}\). Die Idee ist nun, sowohl den Vektor \(\vec{NM}\) als auch \(\vec{PQ}\) zu berechnen und dann zu zeigen, dass beide unabhängig von \(\tau\) kollinear sind. Ich führe noch eine Funktion \(o\) (für orthogonal) ein, wobei \(o(x)\) der um 90° positiv gedrehte Vektor von \(x\) ist. Es gilt also \(b=o(a)\) und \(o(b)=-a\).
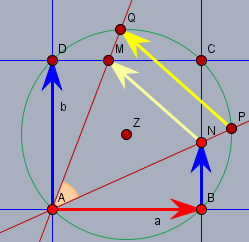
Ich wähle den Punkt \(A\) als 'Ursprung'. Dann sind die Geraden \(g_0\) und \(g_1\) durch \(AN\) und \(AM\)$$g_0: \space x = s (a+\tau b), \quad s \in \mathbb{R}\\g_1: \space x = t (a+ \tau b + o(a+\tau b)) = t(a(1-\tau) + b (1+\tau)), \quad t \in \mathbb{R}$$Damit berechne ich die Vektoren \(\vec{AN}=n\) und \(\vec{AM}=m\). \(n\) ist offensichtlich$$n = a+\tau b$$und \(m\) ist der Schnittpunkt von \(g_1\) und $$g_2: \space x = b + ra $$Gleichsetzen gibt$$\begin{aligned}ta(1-\tau) + tb (1+\tau) &= b + ra \\ (t(1 - \tau) - r)a + (t (1 + \tau) - 1)b &= 0\end{aligned}$$Da \(a\) und \(b\) linear unabhängig sind, müssen die Faktoren =0 sein. Aus dem Faktor vor \(b\) folgt direkt$$t_m (1+\tau) - 1 = 0 \implies t_m = \frac{1}{1 + \tau}$$und damit der Vektor \(m\):$$m = g_1(t_m) = \frac 1{1 + \tau}(a(1-\tau) + b (1+\tau))= a \frac{1-\tau}{1 + \tau} + b$$Somit ist der Vektor \(\vec{NM}\) $$\vec{NM} =m-n = a \frac{1-\tau}{1 + \tau} + b - a-\tau b = a \frac{-2\tau}{1+\tau} + b(1-\tau)$$Ist \(k\) ein beliebiger Vektor von \(A\) auf die Kreislinie und \(z=\vec{AZ}\), so ist $$ (k-z)^2 = z^2, \quad z = \frac 12 (a+b) \\ k^2 - 2kz + z^2 = z^2 \\ k^2 = k(a+b)$$Den Kreis bringe ich mit \(g_0\) und \(g_1\) zum Schnitt, um die Vektoren \(\vec{AP} = p\) und \(\vec{AQ} = q\) zu bestimmen. Dazu setzt man für \(k\) die Gleichung der jeweiligen Gerade ein. Zunächst \(g_0\) für \(p\):$$\begin{aligned} s^2 (a + \tau b)^2 &= s(a + \tau b)(a+b) \\ s(a^2 + 2\tau ab + \tau^2 b^2) &= a^2 + ab(1+\tau) + \tau b^2 \\ s a^2(1 + \tau^2) &= a^2( + \tau) \\ s_p &= \frac {1 + \tau}{1 + \tau ^2} \end{aligned}$$Dann \(g_1\) für \(q\):$$\begin{aligned}t^2(a(1-\tau) + b (1+\tau))^2 &= t(a(1-\tau) + b (1+\tau))(a+b) \\ t(a(1-\tau) + b (1+\tau))^2 &= (a(1-\tau) + b (1+\tau))(a+b) \\ t( a^2(1-\tau)^2 + b^2 (1+\tau)^2) &= a^2 (1-\tau) + b^2 (1+\tau) \\ t( 1+\tau^2) &= 1\\ t_q &= \frac 1{1+\tau^2}\end{aligned}$$Und nun die Differenz \(\vec{PQ}\):$$\begin{aligned} \vec{PQ} &= q-p = g_1(t_q) - g_0(s_p) \\ &= \frac 1{1+\tau^2}(a(1-\tau) + b (1+\tau)) - \frac {1 + \tau}{1 + \tau ^2} (a+\tau b) \\ \quad &= \frac 1{1 + \tau ^2} \left( a(1-\tau) + b (1+\tau) - (1 + \tau )(a+\tau b)\right) \\ \quad &= \frac 1{1 + \tau ^2} \left( -2a\tau + b (1-\tau^2) \right) \\ \quad &= \frac {1+\tau}{1 + \tau ^2} \left( a \frac{-2\tau}{1+\tau} + b (1-\tau) \right) \\ \quad &= \frac {1+\tau}{1 + \tau ^2}\vec{NM} \quad \text{q. e. d.} \end{aligned}$$