Hallo Jani,
(b) bei den das Schattenbild begrenzenden Punkten hast Du den Punkt \(J=(0|-6|2)\) vergessen. Wozu Du den Vektor \(\vec{AH}\) benötigst erschließt sich mir nicht. Er bildet zwar den Stützvektor, aber nur weil zufällig \(A\) im Ursprung liegt. Die Geradengleichung durch \(H\) hast Du richtig aufgestellt: $$g_H = \vec{H} + r \cdot \vec{s} = \begin{pmatrix} 3\\ -3\\ 8\end{pmatrix} + r \cdot \begin{pmatrix} 1\\ -1\\ -1\end{pmatrix}$$ Der Punkt \(S=(11|-11|0)\) - der Schattenpunkt von \(H\) ist ebenfalls richtig.
Von Punkten, die bereits auf der \(x_1x_2\)-Ebene liegen, brauchst Du keinen Schattenpunkt zu berechnen. Das ist immer der Punkt selbst. Die Punkte \(C\) und \(B\) werfen keinen Schatten. Du hast sie auch oben nicht in der Liste aufgeführt.
Es fehlen die Schattenpunkte von \(G\) und \(J\) - das sind \(G'=(8|-2|0)\) und \(J'=(2|-8|0)\).
Um die Behauptung zu prüfen, dass der Schatten von den Geraden \(g_1\) und \(g_2\) eingegrenzt wird, reicht es aus zu zeigen, dass jeweils zwei der Schattenpunkte auf einer der Geraden liegen. Im Fall von \(g_1\) sind das \(S\) und \(J'\) und im Fall von \(g_2\) sind das \(S\) und \(G'\). $$g_1: \space \vec{x} = \begin{pmatrix} 11\\ -11\\ 0\end{pmatrix} + t_1 \cdot \begin{pmatrix} -3\\ 1\\ 0\end{pmatrix}$$
\(S\) liegt auf \(g_1\), da \(S\) identisch zum Stützpunkt von \(g_1\) ist. Um zu zeigen, dass \(J'\) auch darauf liegt, muss es für folgende Gleichung ein \(t_1\) geben, was die Gleichung löst: $$J' = \begin{pmatrix} 2\\ -8\\ 0\end{pmatrix} = \begin{pmatrix} 11\\ -11\\ 0\end{pmatrix} + t_1 \cdot \begin{pmatrix} -3\\ 1\\ 0\end{pmatrix} \\ \implies \begin{pmatrix} -9\\ 3\\ 0\end{pmatrix} = t_1 \cdot \begin{pmatrix} -3\\ 1\\ 0\end{pmatrix} $$ die letzte Zeile ist für jedes \(t_1\) erfüllt. Aus der zweiten Zeile folgt \(t_1 = 3\); einsetzen in die erste Zeile bestätigt dies. Also liegt \(J'\) auf \(g_1\). Mit \(g_2\) geht es genauso.
(c) ich unterstelle, dass der Mann an der Position \(F=(7|-7|0)\) steht. Sonst stände er in der Sonne. Um zu zeigen, dass der Kopf sich im Schatten befindet, muss der Schattenpunkt \(F'=(9|-9|0)\) des Kopfes innerhalb des Schattens liegen. Zeige, dass \(F'\) auf der Verbindunglinie zwischen den Punkten \(S\) und \(E\) liegt.
Ich habe Dir die Szene in Geoknecht3D eingegeben.
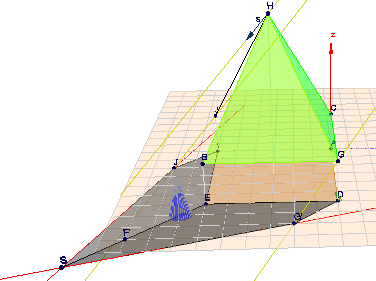
klicke auf das Bild, dann kannst Du die Szene mit der Maus rotieren und bekommst einen besseren räumlichen Eindruck.
Falls noch Fragen offen sind, so melde Dich bitte.
Gruß Werner
Tipp: halte beim Fotografieren das Handy parallel zum Papier und achte auf den Bildausschnitt.