Wie lautet der Achsenabschnitt? Empirische Messungen.

Question

Gegeben sind folgende empirische Messungen:

x₁	6,7	8	10,4	12,1
z₁	12,58	13,09	15,64	16,41

Grafisch liegen diese Punkte folgendermaßen im Koordinatensystem:

Die Beobachtungen liegen ungefähr auf einer linearen Funktion \( z = a_0 + a_1 x \) und sind mit leichten Fehlern behaftet. Ermitteln Sie die Parameter dieser linearen Funktion durch Verwerndung der Normalgleichungen.

Wie lautet der Achsenabschnitt?

Comments

Vom Duplikat:

Titel: Empirische Messungen - wie lautet der Achsenabschnitt?

Stichworte: funktion,lineare-funktionen

Wie lautet der Achsenabschnitt?

Vielen Dank im Voraus!

---

Hallo

 die Formeln für die Normalengleichung habt ihr doch sicher, dann ist es nur Rechnerei, was daran kannst du nicht? Exel macht es auch einfach für dich. Also, wenn du Probleme hast, musst du die genauer sagen, denn einfach deine HA machen ist ja keine Hilfe.

lul

---

Es ist Anfang Dezember. Jedes Jahr um diese Zeit trudeln die Fragen nach dem Achsenabschnitt ein ... Tipp: \(a_0=11,53785486\)

---

xi 4.4 7 8.7 10.6
zi 19.03 19.76 21.54 21.82
das sind meine Werte. Könnte die bitte auch jemand für mich in Excel eingeben? Weiß wirklich nicht was genau ich da in Excel eingeben muss. Vielen Dank schon mal!

---

Weiß wirklich nicht was genau ich da in Excel eingeben muss.

Du hast ja auch nicht danach gefragt ;-). Gib zunächst die \(x_i\) und \(z_i\) ein. Die \(z_i\) heißen bei Excel Y-Werte:

 

Dann gibst Du für \(a_0\) ein (gelb): $$\text{=ACHSENABSCHNITT(B2:E2;B1:E1)}$$ \(\text{B2:E2}\) sind die Y- bzw. Z-Werte und \(\text{B1:E1}\) sind die X-Werte. Und für \(a_1\) (grün) gibst Du ein:$$\text{=STEIGUNG(B2:E2;B1:E1)}$$Das Ergebnis steht dann da: $$a_0 = 16,75648948; \quad a_1= 0,492639808$$ mehr zur Theorie des Themas findest Du hier.

Answer 1

es gibt hier mehrere Möglichkeiten die Aufgabe zu lösen!

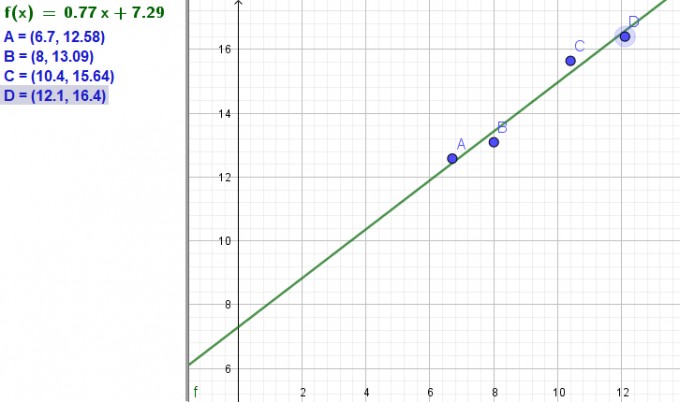
Wenn ich diese Aufgabe so sehe, dann würde ich eine Regression anwenden, aus deinen Datenpunkten resultiert beispielsweise die Gerade:

$$ f(x) = 0,767257x + 7,294509 $$

mit $$ a_0 = 7,29 $$... und $$ a_1 = 0,76... $$

Plot: