Viereck und flächengleiches Parallelogramm

Question

Scheiden Sie drei Ecken eines beliebigen Vierecks ABCD so ab, dass die vier Stücke zu einem Parallelogramm zusammengelegt werden können.

Answer 1

Hallo Roland,

das Viereck sei das Viereck \(ABCD\) wie hier zu sehen ist:

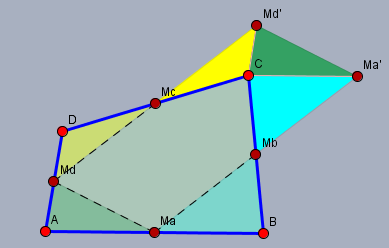
Man halbiere alle Seiten und schneide entlang von drei Verbindungslinien der Seitenmitten drei Ecken ab. Bei der stehen gebliebenen Ecke (hier \(C\)) lege man die benachbarten Dreiecke so an, dass die Position der benachbarten Seitenmitten (hier \(M_b\) und \(M_c\)) erhalten bleibt. Die dritte - gegenüberliegende Ecke - verschiebt man um die Diagonale (hier \(AC\)).

Das fertige Parallelogramm ist \(M_aM_a'M_d'M_d\).

Gruß Werner