Hallo,
Der Mittelpunkt \(M\) zweier Punkte \(A\) und \(B\) berechnet sich aus$$M = \frac 12 (A + B)$$also ist hier $$M_a = \frac 12 \left( A + B\right) = \frac 12 \left( \begin{pmatrix}3\\ 7\\ 4\end{pmatrix} + \begin{pmatrix}1\\ 5\\ 0\end{pmatrix}\right) = \begin{pmatrix}2\\ 6\\ 2\end{pmatrix}$$ genauso lassen sich die anderen Mittelpunkte \(M_b\), \(M_c\) und \(M_d\) berechnen. Um festzustellen, ob das Viereck \(M_aM_bM_cM_d\) ein Parallelogramm ist, kann man entweder die beiden Vektoren$$\vec{M_aM_b} = M_b - M_a = \begin{pmatrix}0.5\\ -3\\ 1\end{pmatrix} \\ \vec{M_dM_c} = M_c - M_d = \begin{pmatrix}0.5\\ -3\\ 1\end{pmatrix}$$vergleichen. Sind sie identisch - so wie hier - so ist das Viereck ein Parallelogramm. Oder man berechnet wieder die Mittelpunkte diesmal von den gegenüberliegenden Ecken des Vierecks$$M_1 = \frac 12 (M_a + M_c) = \begin{pmatrix}3.5\\ 4\\ 2.75\end{pmatrix} \\ M_2 = \frac 12(M_b + M_d) = \begin{pmatrix}3.5\\ 4\\ 2.75\end{pmatrix}$$fallen diese zusammen, ist das Viereck ebenso ein Parallelogramm.
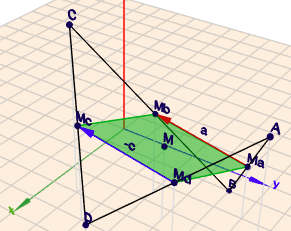
(klick auf das Bild, dann öffnet sich die Szene im Geoknecht3D)
Diese Eigenschaft gilt übrigens für beliebige vier Punkte im Raum.