es gibt für Umkreis und Inkreis Formeln, da setzt Du die Koordinaten ein und rechnest dann den Um- und Inkreismittelpunkt aus. In diesem besonderen Fall ist es aber so, dass das Dreieck nicht nur gleichschenklig ist, sondern seine Symmetrieachse auch noch auf der \(x=1\)-Linie liegt. D.h. bereits, dass die X-Koordinate sowohl des Um- als auch des Inkreises \(=1\) ist.
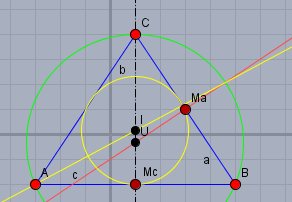
Die Y-Koordinate rechnet man für den Umkreis über die Mittelsenkrechte \(m_a\) von z.B. \(BC\) $$\begin{aligned}m_{a}: \space y &= \frac{|McB|}{|CM_c|} (x - M_{ax}) + M_{ay} \\ &=\frac{\frac 12 (B_x - A_x)}{C_y -B_y}(x - M_{ax}) + M_{ay} \end{aligned}$$ \(M_a\) ist der Mittelpunkt der Strecke \(BC\); also $$M_a = \frac 12 \begin{pmatrix} B_x + C_x& B_y + C_y\end{pmatrix} = \begin{pmatrix} 3& 1\end{pmatrix}$$ Daraus folgt dann $$m_{a}: \space y = \frac{\frac 12 (5 - (-3))}{4 -(-2)}(x - 3) + 1 = \frac 23 (x-3) + 1 = \frac23 x-1 $$ Durch Einsetzen von \(x=1\) (s.o.) kommt man auf den Umkreismittelpunkt $$u_x= 1; \space u_y = -\frac13 $$
Da Du \(\alpha = 56,31°\) bereits berechnet hast, reicht es daraus, die Strecke \(|M_cI|\) zu bestimmen. Es ist $$\tan \frac \alpha 2 = \frac{|M_cI|}{|AM_c|} \\ \implies |M_cI| = \tan \frac \alpha 2 \cdot |AM_c| = \tan 28.155° \cdot 4 \approx 2,141$$ Die Koordinate von \(I\) ist demnach $$i_x = 1; \space i_y = M_{cy} + 2,141 = 0,141$$ Gruß Werner