Winkelhalbierende im Viereck

Question

Gegeben sei ein beliebiges Viereck. Je zwei benachbarte Halbierende der Innenwinkel  schneiden sich in einem Punkt. Zeigen Sie, dass diese vier Schnittpunkte Eckpunkte eines Sehnenvierecks sind.

Comments

Anwendung des Außenwinkelsatzes;

(α/2 + β/2)+(γ/2 + δ/2)=180°.

---

An die Moderatoren: Bitte den obigen Kommentar NICHT ohne Zustimmung des Autors in eine Antwort umwandeln.

Answer 1

Hallo Roland,

Das ist leicht, aber eine Antwort hat noch keiner geschrieben. Also bitte:

 

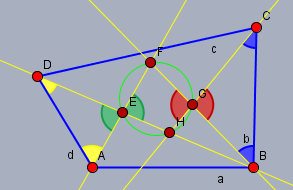
der grüne Winkel bei \(E\) sei \(\alpha\) und der rote bei \(G\) sei \(\gamma\). Die Summe der gelben Winkel sei \(g\) und die Summe der blauen Winkel sei \(b\). Dann ist $$\alpha = \pi - g \\ \gamma = \pi - b$$ Beide Gleichungen addieren gibt $$\alpha + \gamma = 2\pi - (g+b) = 2 \pi - \pi = \pi$$ da die Summe \((g+b)\) die Hälfte der Winkelsumme im Viereck ist. Also ist in dem Viereck \(EFGH\) die Winkelsumme zweier gegenüberliegenden Winkel gleich \(\pi\) und somit ist es ein Sehnenviereck.

Gruß Werner