Beweis der Matrizen Multiplikation in Kästchenform

Question

Ich musste folgende Aufgabe bearbeiten und würde gerne wissen ob mir die Bearbeitung gelungen ist.

Aufgabe:

$$\text{Seien } p,q \in \mathbb{N}; n:= p+q ; A,B \in \text{ Mat}(n;K) \text{ quadratische Matrizen in Kästchenform:}$$

$$\text{ mit } A_1,B_1 \in \text{Mat}(p;K),A_2,B_2 \in \text{Mat}(p,q;K),A_3,B_3 \in \text{Mat}(q,p;K)\\\text{ und } A_4,B_4 \in \text{Mat}(q;K)$$

Zu beweisen ist folgende Regel:

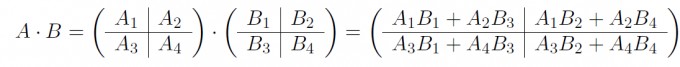
Problem/Ansatz:

In der Vorlesung hatten wir folgende Fomel zur Matrizenmultiplikation bewiesen:

$$K^{m \times n}\times K^{n\times p} \longrightarrow K^{m \times p} \\(A,B) \longrightarrow A*B\\\text{mit } C:= AB \in \mathbb{K}^{m \times p}$$

Meine Idee wäre eine Transferleistungen auf diese Aufgabe zu machen.

Beweisweg:

$$\text{ Seien:} \\\{C^{1 \times 1} := A_1B_1 + A_2B_3\}, \{C^{1 \times 2}:= A_1B_2+A_2B_4\} ,\\  \{ C^{2 \times 1}:= A_3B_1+A_4B_3\},  \{ C^{2 \times 2}:= A_3B_2+A_4B_4\} \land (x\in (\{p\},\{q\})\in n): (A_i,B_j)^{ \exists! x \times \exists! x}\neq (A_i,B_j)^{ x \times  x} \\\text{mit } C:=\begin{pmatrix} C^{1 \times 1} & C^{1 \times 2} \\ C^{2 \times 1} & C^{2 \times 2} \end{pmatrix} \\[20pt]\text{Zu zeigen:} \\C^{1 \times 1}\in K^{x \times x} \\C^{1 \times 2}\in K^{x \times x} \\C^{2 \times 1}\in K^{x \times x} \\C^{2 \times 2}\in K^{x \times x} \\\Longrightarrow C \in K^{n \times n} \\[30pt]\text{Beweis:} \\K^{p \times p}\times K^{p\times p} \longrightarrow K^{p \times p} \land K^{p \times q}\times K^{q\times p} \longrightarrow K^{p \times p} \\(A_1,B_1) \longrightarrow A_1*B_1 \land (A_2,B_3) \longrightarrow A_2*B_3 \\\Longrightarrow \{ A_1*B_1 + A_2*B_3\} \in K^{p \times p} \Longleftrightarrow C^{1 \times 1}\in K^{p \times p} \\[20pt]K^{p \times p}\times K^{p\times q} \longrightarrow K^{p \times q} \land K^{p \times q}\times K^{q\times q} \longrightarrow K^{p \times q} \\(A_1,B_2) \longrightarrow A_1*B_2 \land (A_2,B_4) \longrightarrow A_2*B_4 \\\Longrightarrow \{ A_1*B_2 + A_2*B_4\} \in K^{p \times q} \Longleftrightarrow C^{1 \times 2}\in K^{p \times q} \\[20pt]K^{q \times p}\times K^{p\times p} \longrightarrow K^{q \times p} \land K^{q \times q}\times K^{q\times p} \longrightarrow K^{q \times p} \\(A_3,B_1) \longrightarrow A_3*B_1 \land (A_4,B_3) \longrightarrow A_4*B_3 \\\Longrightarrow \{ A_3*B_1 + A_4*B_3\} \in K^{q \times p} \Longleftrightarrow C^{2 \times 1}\in K^{q \times p} \\[20pt]K^{q \times p}\times K^{p\times q} \longrightarrow K^{q \times q} \land K^{q \times q}\times K^{q\times q} \longrightarrow K^{q \times q} \\(A_3,B_2) \longrightarrow A_3*B_2 \land (A_4,B_4) \longrightarrow A_4*B_4 \\\Longrightarrow \{ A_3*B_2 + A_4*B_4\} \in K^{q \times q} \Longleftrightarrow C^{2 \times 2}\in K^{q \times q} \\[20pt]\{ \{C^{1 \times 1}\in K^{p \times p}\} \land \{C^{1 \times 2}\in K^{p \times q} \}\land \{C^{2 \times 1}\in K^{q \times p}\} \land \{C^{2 \times 2}\in K^{q \times q} \}\} \\\land \{ \{C^{1 \times 1}\in K^{p \times p}\} \neq \{C^{1 \times 2}\in K^{p \times q} \}\neq \{C^{2 \times 1}\in K^{q \times p}\} \neq \{C^{2 \times 2}\in K^{q \times q} \}\} \\\Longrightarrow C \in K^{n \times n} \blacksquare$$

Meine Fragen ist die Folgende:

Macht meine Beweisführung Sinn?

Ist sie mathematisch didaktisch korrekt?

Ich hatte Probleme den Beweisanfang ( was zur Zeigen) und Endaussage zu erstellen, ist es mir gelungen?

Answer 1

In der Vorlesung hatten wir folgende Fomel zur Matrizenmultiplikation bewiesen:

Das ist keine Formel, die bewiesen wurde. Das sind die formalen Anforderungen, die erfüllt sein müssen damit Matrizen multipliziert werden können. Es wird darin eigentlich nur gefordert, das man m×n-Matrizen und n×p-Matrizen "multiplizieren" kann und das Ergebnis dieser Multiplikation eine m×p-Matrix ist.

Wie die Multiplikation konkret durchgeführt wird, wird nicht erwähnt. Darauf müsstest du dich aber beziehen um die Behauptung zu zeigen.

Seien

        \(A = (a_{i,j})_{\substack{1\leq i\leq n\\1\leq j\leq n}}, B = (b_{i,j})_{\substack{1\leq i\leq n\\1\leq j\leq n}} \in K^{n\times n}\).

Dann ist

        \(A\cdot B = \left(\sum_{k=1}^n a_{i,k}b_{k,j}\right)_{\substack{1\leq i\leq n\\1\leq j\leq n}}\)

Sei nun \(C = A\cdot B\) mit \(C = (c_{i,j})_{\substack{1\leq i\leq n\\1\leq j\leq n}}\)  und \(p\in\mathbb{N}\) mit \(1\leq p \leq n\) und

        \(\begin{aligned} A_1 &= (a_{i,j})_{\substack{1\leq i\leq p\\1\leq j\leq p}}\\ A_2 &= (a_{i,j})_{\substack{1\leq i\leq p\\p+1\leq j\leq n}}\\ B_1 &= (b_{i,j})_{\substack{1\leq i\leq p\\1\leq j\leq p}}\\ B_3 &= (b_{i,j})_{\substack{p+1\leq i\leq n\\1\leq j\leq p}} \end{aligned}\).

Ferner sei \(D_1 = A_1 B_1 + A_2 B_3\) mit \(D_1 = (d_{i,j})_{\substack{1\leq i\leq p\\1\leq j\leq p}}\).

Zeige dass \(c_{i,j} = d_{i,j}\) für alle \(i,j\) mit \(1\leq i\leq p\) und \(1\leq j\leq p\) ist. Damit hättest du das linke obere Kästchen des bewiesen. Verfahre genau so für die drei übrigen Kästchen.