Analytische Geometrie: Koordinatenform ablesen?

Question

ich habe eine Matheaufgabe im über das Themengebiet Analytische Geometrie alles mit Ebenen und deren Gleichungen etc.

Leider ist bei mir das Problem , dass ich alles Theoretische sehr gut kann , aber bei so Anwendungsaufgaben wie diese, weiß ich nie was man von mir will.

Die Aufgabe :

a)Um im Winter ein kontrolliertes Abrutschen der Schneemassen zu gewährleisten, sind die Stützen eines ebenen Carportdaches ver schieden lang Während zwei diagonal gegenüberliegende Pfosten die Länge 4 m haben, ist der dritte mit 5 m etwas länger Wie lang muss die vierte Stütze sein, damit das Dach fest aufliegt?

 B)Das Dach kann als Teil einer Ebene aufge- fasst werden. Zeigen Sie, dass analog zu der Parametergleichung einer Geraden eine Koordinatenebene für diese Ebene aufgestellt werden kann. Bestimmen Sie mithilfe dieser Gleichung die Koordinaten des Punktes D. Erläutern Sie an einem Beispiel, wie man überprüfen kann, ob ein vorgegebener Punkt in der Ebene liegt.

C) Auf dem Dach des Carports werden Solarmodule zur Energiegewinnung montiert. Solarmodule generieren am meisten Energie, wenn sie senkrecht vom Sonnenlicht getroffen werden.Geben Sie einen Vektor n an, der senkrecht auf der Dachebene steht. Begründen Sie, dass mithilfe des Vektors n die Dachebene durch die Gleichurg  E: 3x+4y+24z-120 =0 dargestellt werden kann Tipp: Überlegen Sie, wie für einen beliebigen Punkt X in der Ebene E die Vektoren AX und n zueinander liegen.

Problem/Ansatz:

a) das verstehe ich nicht ganz. Soll ich das berechnen oder mir denken? Also ich hätte jetzt gesagt , dass der vierte Pfosten dann auch 5m lang ist , damit das ganze stabil stehen kann. Oder was soll ich da machen?

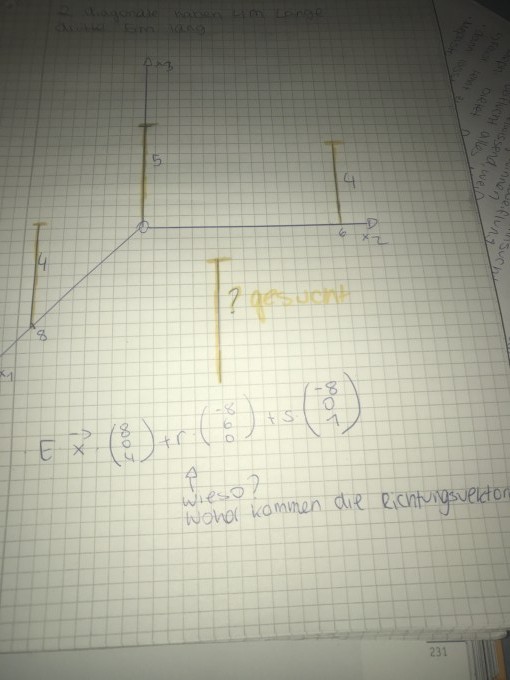
B) Und in der Stunde hatten wir diese Ebenengleichung zu dem ganzen notiert ( siehe Anhang) . Ich versteh nicht wie man auf diese Richtungsvektoren kommt, welche Vektoren sind das? Der rest ist mir klar mit der Ebenengleichung erstmal die Normalenform und dnan die Koordinatenform bilden... und wie berechne ich Punkt D?

C) ist das nicht einfach, dass man eben einen normalvektor hat, aus dem man eben die koordinatenform ablesen/bilden kann? Mehr ist es doch nicht?

Ich würde euch wirklich sehr danken wenn ihr mir das versuchen würdet zu erklären, als Weihnachtsgeschenk

I

Comments

Da liegen also 4 Stangen 2 mit 4m und eine mit 5 m. Gut, aber sollten wir nicht auch wissen, wo wir Löcher graben sollen um die Stangen aufzustellen?

---

Hallo Wächter

das muss man für die Höhe des 4ten Pfosten nicht wissen nur dass es ein Rechteck ist.

Gruß lul

---

Sorry dass ich nerve , aber ich wäre dankbar wenn du mir das allerletze mal hilft
ich habe also die Ebenengleichung
E: \( \begin{pmatrix} 8\\0\\4 \end{pmatrix} \) + r • \( \begin{pmatrix} -8\\6\\0\end{pmatrix} \) + s• \( \begin{pmatrix} -8\\0\\1 \end{pmatrix} \)

Wenn ich jetzt die Länge also den x₃-Wert berechnen will geh ich wie folgt vor:
Die vierte Stütze hat X1 Wert = 0 und x2-Wert=2
R bzw. S durch Gleichungsystem bestimmen
d.h
0=8+r•(-8)+s•(-8)
—>dann r hier einsetzen. Dann folgt daraus s = \( \frac{2}{3} \)
2=0+r•6+s•0
—>daraus folgt r=  \( \frac{1}{3} \)
x₃= 4+r• 0 + s• 1
—> r und s hier einsetzen dann kommt als x₃ = \( \frac{14}{3} \) raus , also 4,666666
Damit ist sie doch nicht kürzer als alle anderen Pfosten, wie du gesagt hast , oder hab ich mich bei der Rechnung vertan?

Danke für deine Hilfe!!!

Answer 1

Hallo

der 4te Pfosten muss kürzer als alle anderen sein, Wenn er 5m hoch wäre kann man keine Ebene mehr durch die 4 Punkte legen. d.h. du musst erst die Grundfläche wie in deiner Zeichnung festlegen, dann eine Ebene durch die 3 Punkte legen, und der vierte Punkt, von dem du ja die x und y Koordinate kennst muss in der Ebene liegen. man kann es sich auch vorstellen: von dem 5m Pfosten geht es bis zur Mitte 1m nach unten, dann muss es bis aussen auch einen weiteren m nach unten gehen.

b) die Richtungsvektoren sind die von den

oberen Enden des 5m Pfostens zu den 2 4m Pfosten, deine Mitschrift kann ich nicht lesen.

die Ebene kannst du auch in a) benutzen.

c) du sollst ja begründen, dass n*x=Zahl eine Darstellung der Ebene ist. weil jeder Vektor x der darin liegt senkrecht auf n steht.

Comments

Jetzt macht es sinn.. wirklich vielen dank!!!

---

Du hast jetzt gesagt die Richtungsvektoren gehen von dem 5m langen Pfosten zu den zwei 4 m Pfosten...

in der schule haben wir uns diese Ebenengleichung aufgeschrieben( falls man es auf dem Bild nicht erkennt) :

E : (8|0|4) + s * (-8|6|0) + v* (-8|0|1)

( das sind übrigens Vektoren)

Laut dieser Ebenengleichung ist der Stützvektor ja der linke 4 m Pfosten und die Richtungsvektoren dazu, naja die machen halt kein sinn .. das was du sagst würde mehr sinn machen , und so dachte ich erstmal auch .

---

Hallo

meine Idee war bei dem 5m anzufangen, aber man kann irgendeinen als Stützvektor nehmen und irgend 2 Vektoren zwischen 2 Punkten, die Ebenengleichung sieht dann verschieden aus, enthält aber dieselben Punkte. kurz irgendein Punkt der Ebene und irgend 2 Vektoren in der Ebene bestimmen sie.

Gruß lul

---

Sorry dass ich nerve , aber ich wäre dankbar wenn du mir das allerletze mal hilft

ich habe also die Ebenengleichung

E: \( \begin{pmatrix} 8\\0\\4 \end{pmatrix} \) + r • \( \begin{pmatrix} -8\\6\\0\end{pmatrix} \) + s• \( \begin{pmatrix} -8\\0\\1 \end{pmatrix} \)

Wenn ich jetzt die Länge also den x₃-Wert berechnen will geh ich wie folgt vor:

Die vierte Stütze hat X1 Wert = 0 und x2-Wert=2

R bzw. S durch Gleichungsystem bestimmen

d.h

0=8+r•(-8)+s•(-8)

—>dann r hier einsetzen. Dann folgt daraus s = \( \frac{2}{3} \)

2=0+r•6+s•0

—>daraus folgt r=  \( \frac{1}{3} \)

x₃= 4+r• 0 + s• 1

—> r und s hier einsetzen dann kommt als x₃ = \( \frac{14}{3} \) raus , also 4,666666

Damit ist sie doch nicht kürzer als alle anderen Pfosten, wie du gesagt hast , oder hab ich mich bei der Rechnung vertan?

Danke für deine Hilfe!!!