Matrix lineare Abbildung f: V -> W

Question

Aufgabe:

Seien V,W Vektorräume und

$$B = b _ { 1 } , b _ { 2 } , b _ { 3 } , \tilde { B } = \tilde { b } _ { 1 } , \tilde { b } _ { 2 } , \tilde { b } _ { 3 } , C = c _ { 1 } , c _ { 2 } , \tilde { C } = \tilde { c } _ { 1 } , \tilde { c } _ { 2 }$$

Basen von V und W mit

$$\tilde { B } ^{M _ { B }} \left( \mathrm { id } _ { V } \right) = \left( \begin{array} { l l l } { 1 } & { 1 } & { 1 } \\ { 0 } & { 1 } & { 1 } \\ { 0 } & { 0 } & { 1 } \end{array} \right), \tilde { C } ^ { M _ { C } \left( \mathrm { id } _ { W } \right) } = \frac { 1 } { 2 } \left( \begin{array} { c c } { 1 } & { - 1 } \\ { 1 } & { 1 } \end{array} \right) $$

Eine lineare Abbildung von f: V → W sei durch

$$\tilde { B } ^ { M } \tilde { C } ( f ) = \left( \begin{array} { c c c } { 2 } & { 4 } & { 2 } \\ { 1 } & { - 1 } & { 0 } \end{array} \right)$$

gegeben.

Bestimmen Sie

$$B ^ M _ { \tilde { B } } \left( \mathrm { id } _ { V } \right) , \tilde { C } ^ { M _ { C } \left( \mathrm { id } _ { W } \right) }$$

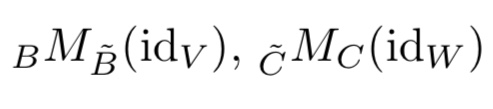
und anschließend

$$ _{B} M _ { C } ( f )$$

Ich sitze mittlerweile seit einer Stunde an dieser Aufgabe und komme einfach nicht weiter. Kann mir jemand einen Impuls geben wie man an diese Aufgabe herangehen sollte?

Answer 1

Die Matrix B M Bschlange von idV ist die Inverse von Bschlange M B von idV, also

1  -1  0
0  1   -1
0  0    1

und entsprechend die zweite

1      1
-1    1

und für _B M _C (f)    brauchst du diese wohl nur von

rechts und links an die gegebene dran zu multiplizieren.