Den Funtionsterm bestimmen

Question

Die Aufgabe lautet: Der Graph einer ganzrationalen Funktion vierten Grades ist symmetrisch zur y-Achse. Er hat in P(2/0) die Steigung 2 und bei -1 eine Wendestelle. Bestimmen Sie den Funktionsterm. Ich habe diese Funktion ausgestellt: f(x)= ax^4 + bx^2 + c Die Punkte habe ich aus dem Text herausgefunden: f'(2)=2 f(2)=0 f''(-1)=0 Sind das alle Punkte oder habe ich einen vergessen, bzw. welche falsch? Danach habe ich I. 2=32a+4b II. 0=16a+4b+c III. 0=-12a+2b Wie kann ich jetzt weiter vorgehen, um den Funktionsterm zu bestimmen?   :)

Answer 1

Die Aufgabe lautet:

Der Graph einer ganzrationalen Funktion vierten Grades ist symmetrisch zur y-Achse.

f(x) = ax^4 + bx^2 + c

Er hat in P(2/0)

f(2) = 0
16·a + 4·b + c = 0

die Steigung 2

f'(2) = 2
32·a + 4·b = 2

und bei -1 eine Wendestelle.

f''(1) = 0
12·a + 2·b = 0

Wir nehmen die beiden Gleichungen

32·a + 4·b = 2
12·a + 2·b = 0

I - 2*II

8·a = 2
a = 1/4

32·(1/4) + 4·b = 2
b = -3/2

16·(1/4) + 4·(-3/2) + c = 0
c = 2

Damit hat mal alle Unbekannten und die Funktion lautet

f(x) = 1/4*x^4 - 3/2*x^2 + 2

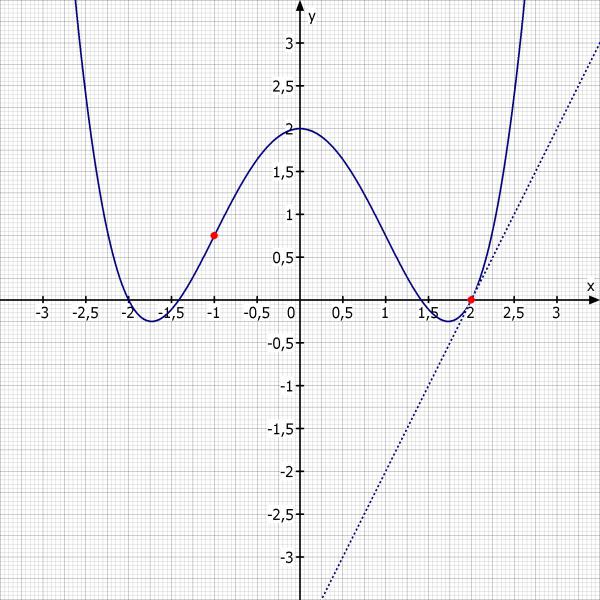
Skizze:

Answer 2

 

 

f(x) = ax⁴ + bx² + c

f'(x) = 4ax³ + 2bx

f''(x) = 12ax² + 2b

 

I. f(2) = 0 = 16a + 4b + c

II. f'(2) = 2 = 32a + 4b

III. f''(-1) = 0 = 12a + 2b

 

Soweit habe ich dieselben Gleichungen wie Du, aber bei der 3. Gleichung hast Du einen Vorzeichenfehler: 

f''(-1) = 0 = 12a(-1)² + 2b = +12a + 2b

 

3 Gleichungen, 3 Unbekannte!

 

II. - III.*2

8a = 2 | a = 1/4

Eingesetzt in III.

0 = 3 + 2b | b = -3/2

Eingesetzt in I.

0 = 4 - 6 + c | c = 2

 

Die gesuchte Funktion heißt also

f(x) = 1/4 * x⁴ - 3/2 * x² + 2

 

Probe: 

f(2) = 1/4 * 16 - 3/2 * 4 + 2 = 4 - 6 + 2 = 0

f'(x) = x³ -3x

f'(2) = 8 - 6 = 2

f''(x) = 3x² - 3

f''(-1) = 3 - 3 = 0

Passt :-)

 

Besten Gruß