Aufgabe:
Der Verlauf des Erdöl- und Erdgaspreises können durch eine quadratische und eine kubische Parabel für einen Zeitraum von 12 Monaten modelliert werden. Erdölpreis in $ pro Barrel, Gaspreis äquivalent. Der Erdgaspreis wird durch die Funktion f(x) = 0,01x³ - 0,94x + 90 beschrieben.
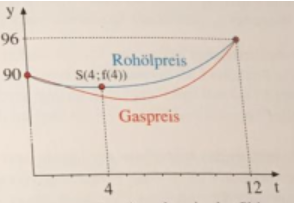
a) Bestimmen Sie den Funktionsterm des Erdölpreises aus den Angaben in der Skizze.
b) In welchem Monat überholt der Öl- den Gaspreis?
c) Wie hoch waren die minimalen Preise jeweils im Jahresvergleich?
d) Wie hoch war die mittlere jährliche Preissteigerungsrate jeweils?
e) Wann war die Preissteigerungsrate beim Erdgas maximal, wie hoch war sie?
f) Zu welchem Zeitpunkt war die Preisdifferenz Öl/Gas am größten?
Ansatz:
Wer könnte mir helfen, solche und ähnliche Aufgaben kommmen in der nächsten KA dran. Ich vermute mal, dass die Funktion des Rohölpreises hier eine quadratische sein soll, aber so eindeutig steht das gar nicht da. Ich habe versucht, die Funktion über die Scheitelpunktform zu ermittel, da S sicherlich der Scheitelpunkt sein soll. Ich bekomme aber nicht die 2 y-Werte 90 und 96 $ in die Funktion. Wie könnte mir die Funktion, die den Rohölpreis abbildet, ermitteln und erklären, wie man da vorgeht?