Ein Haus sei gegeben durch:
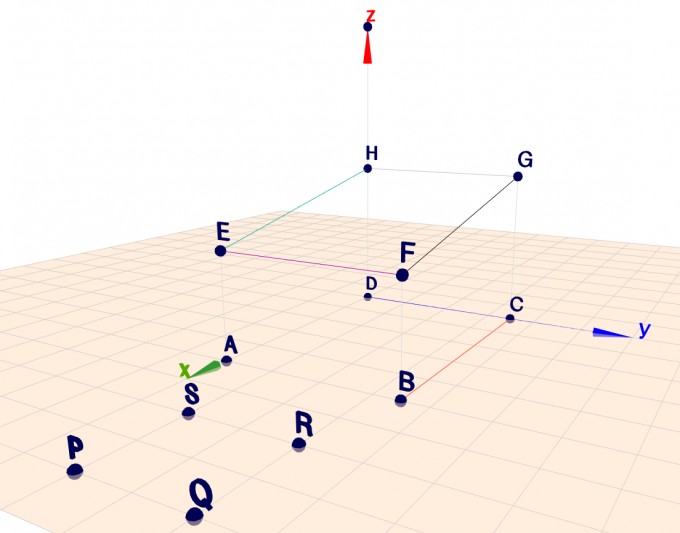
A(5|0|0), B(5|3,5|0), C(0|3.5|0), D(0|0|0), E(5|0|2), F(5|3.5|2), G(0|3.5|3)
Vor dem Haus steht ein Sandkasten, der durch P(9|1|0), Q(9|3|0), R(7|3|0), S(7|1|0) beschrieben wird.
6m vertikal über dem Punkt D ist eine Lampe plaziert.
Aufgabe (ausgedacht von mir):
Wie groß ist der vom Licht bedeckte Flächeninhalt des Sandkastens?
Ansatz:
(1) Geradengleichung für Lichstrahlen aufstellen
(2) Spurpunkt der \(xy\)-Ebene der Geraden berechnen
(3) Geradengleichung aus den beiden Spurpunkten aufstellen
(4) Geradengleichungen mit \(QR\) und \(PQ\) aufstellen
(5) Schnittstellen der Spurgerade aus (3) und den Geraden aus (4)
(6) Flächeninhalt berechnen
Bevor ich anfange mit dieser Rechnung, geht das denn überhaupt so, wie ich denke?
Grüße