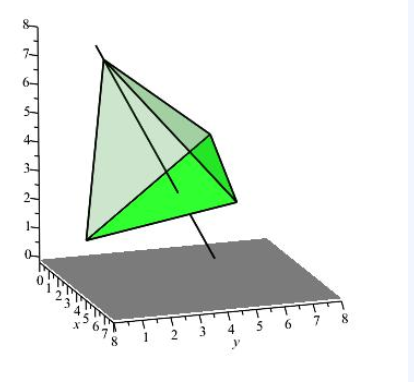
Ein regelmäßiges Tetreder ist ein Körper mit vier gleichseitigen Dreiecken als Außenflächen. Die Abbildung zeigt ein regelmäßiges Tetraeder, die grüne Bodenfläche hat die Ecken A=(2;1;1), B=(6;5;3) und C=((8−√54)/5;6;(4+√216)/5)
1. Bestimmen Sie zunächst den Schwerpunkt der Bodenfläche.
2. Berechnen Sie anschließend die Höhe des Tetraeders. Tipp: Für die Höhe h des Tetreders gilt: h=(√6/3)⋅a, wenn a die Länge der Kanten des Tetraeders ist.
3.Bestimmen Sie nun die Koordinaten der Spitze des Tetraeders. Tipp: Die Spitze des Tetraeders befindet sich senkrecht oberhalb des Schwerpunktes der Bodenfläche.
Ansatz:
1. SP= 1/3*(a+b+c)= (2.71,4,2.58)
2. h= (√6/3)*a= (√6/3)*6=4.90
3. Geraden gleichung Aufstellen?
danke im voraus.
.
Berechnen Sie die Koordinaten der Spitze des Tetreders. Die z-Koordinate soll positiv sein.