Für welche Parameter a ∈R schließt eine Gerade mit dem Richtungsvektor v eine Ebene mit einem Winkel von 45° ein?

Question

Aufgabe: Gesucht sind die Parameter a ∈R für die eine Gerade mit dem Richtungsvektor v = (a|-2|a) einen Winkel von 45° mit der Ebene einschließt, in der sich das Dreieck ABC (aus vorheriger Aufgabe) befindet.

Das Dreieck ABC besteht aus diesen drei Punkten : A(5|3|1) , B(3|2|1) , C(1|0|2).

Wie komme ich jetzt genau auf die Parameter?

Answer 1

Wie komme ich jetzt genau auf die Parameter?

Du bestimmst zunächst den Normalenvektor der Ebene und anschließend bestimmst Du den Parameter $a$ so, dass der Winkel von $\vec{v}=(a|-2|a)^T$ zum Normalenvektor $90°-45°=45°$ beträgt.

Den Normalenvektor erhält man über das Kreuzprodukt: $$\vec{n} = (B-A) \times (C-A) = \begin{pmatrix} -2\\ -1\\ 0 \end{pmatrix} \times \begin{pmatrix} -4\\-3 \\ 1\end{pmatrix} = \begin{pmatrix} -1\\ 2\\ 2\end{pmatrix}$$ Den Winkel $\alpha$ bekommt man über das Skalarprodukt. Es gilt: $$\vec{v} \cdot \vec{n} = |\vec{v}|\cdot |\vec{n}| \cdot \cos \alpha$$Jetzt einsetzen, was wir wissen: $$\begin{pmatrix} a\\ -2\\ a\end{pmatrix} \cdot \pm \begin{pmatrix} -1\\ 2\\ 2\end{pmatrix} = \sqrt{2a^2+4} \cdot \sqrt{9} \cdot \cos 45°$$ Das $\pm$ habe ich eingefügt, weil nicht angegeben ist, auf welcher Seite der Ebene sich die $45°$ befinden sollen. Es sind also zwei Lösungen für $a$ zu erwarten. Weiter auflösen: $$\begin{aligned} \pm(a-4) &= \sqrt{2a^2+4} \cdot \frac32 \sqrt{2} \\a^2- 8a +16 &= (2a^2+4) \cdot \frac 92 \\ 2a^2 -16a + 32 &= 18a^2 + 36 \\ 16a^2 +16a + 4&= 0 \\ a^2 + a + \frac 14 &= 0\\ \implies a_{1,2} &= -\frac 12 \pm \sqrt{\frac 14 - \frac 14} = - \frac 12\end{aligned}$$die beiden Lösungen fallen also zusammen. Und in Geoknecht3D sieht das so aus:

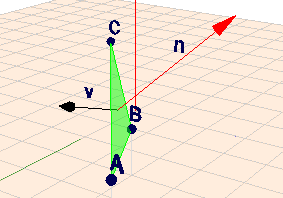
Gruß Werner

Answer 2

Hallo

 aus den 3 Punkten die Koordinatenform der Ebene bestimmen, dann kennst du den Normalenvektor,  wenn der einen Winkel von 45° mit v bildet dann auch v mit der Ebene. weil 90_45=45

Gruß lul