Hallo SilverA,
beim impliziten Eulerverfahren musst Du folgende Gleichung nach \(u_{k+1}\) auflösen: $$u_{k+1} = u_k + h \cdot u'(t_{k+1}, u_{k+1})$$ \(h\) ist das Delta um das \(t\) mit jedem Schritt vergrößert wird. Der Ausdruck \(u_{k+1}\) kommt zweimal vor, ist also nur implizit gegeben. Daher der Name.
In Deinem Fall ist das: $$u_{k+1} = u_k + h \cdot (t_{k+1} - u_{k+1}^2) \\ \implies u_{k+1(1,2)} = \frac 1{2h}\left( -1 \pm \sqrt{1 + 4h(u_k + h t_{k+1})}\right)$$wenn man das nicht 'geschlossen' lösen könnte, dann wäre das Newton-Verfahren von Nöten. Ist hier aber nicht der Fall, da es 'nur' eine Quadratische Gleichung ist.
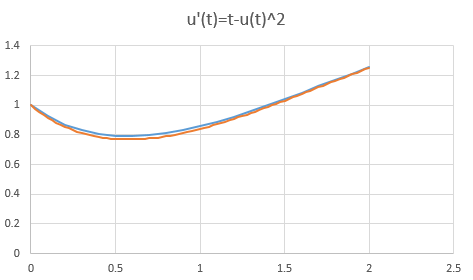
Ich habe das für ein \(h=0,1\) (blau) und ein \(h=0,025\) (orange) im Intervall \(t=[0;2]\) durchgerechnet. Die beiden Kurven zeigen das Ergebnis:
Gruß Werner