Hallo Juli,
ich glaube, Du verwechselst da was. Eine Geradengleichung für die Gerade in der sogenannten Parameterform sieht so aus:$$g: \space \vec{x} = \vec{p} + t \cdot \vec{v} $$Schau Dir dazu folgendes Bild an:
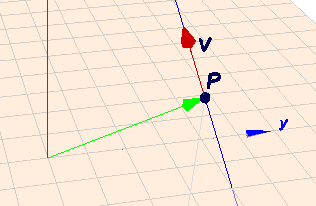
Der Vektor \(\vec{p}\) geht vom Ursprung zu einem Punkt \(P\) der Geraden. Von dort aus, gibt der Vektor \(\vec{v}\) vor, in welche Richtung (im Raum) die Gerade verläuft. Klicke auf das Bild und drehe die Szene mit der Maus, dann bekommst Du einen räumlichen Eindruck.
In Deinem Fall ist: $$g: \space \vec{x} = \vec{p} + t \cdot \vec{v} = \begin{pmatrix} 4\\ 2 \\ 4\end{pmatrix} + t \cdot \begin{pmatrix} 1\\ -1\\ 2\end{pmatrix}$$Beide Vektoren können 'irgendwie' verlaufen, sie müssen nicht zwangsläufig senkrecht aufeinander stehen.
... Reihenfolge ändern und Vorzeichen ändern, ...
Das macht man genau dann, wenn man zu einem Vektor einen anderen sucht, der senkrecht auf dem ersten steht. Angenommen Du suchst einen Vektor, der zu \(\vec{p}\) senkrecht steht. Dann vertauscht man zwei der drei Koordinaten,. und negiert eine der beiden. Die dritte Koordinate setzt man zu 0. Also z.b:
$$\vec{v} = \begin{pmatrix} 4\\ 2 \\ 4\end{pmatrix} \space \to \vec{v}^\perp = \begin{pmatrix} -2\\ 4 \\ 0\end{pmatrix}$$Warum ist das so? Wenn man von beiden Vektoren das Skalarprodukt bildet, dann kommt 0 heraus. Hier ist$$\vec{v} \cdot \vec{v}^\perp = 4 \cdot(-2) + 2\cdot 4 +4\cdot 0 = -8 + 8=0$$Sie stehen also senkrecht aufeinander; das hat aber mit einer Geraden zunächst nichts zu tun. Warum das immer so ist, sieht man, wenn man es verallgemeinert. $$\vec{u} = \begin{pmatrix} x\\ y \\ z\end{pmatrix} \space \to \vec{u}^\perp = \begin{pmatrix} -y\\ x \\ 0\end{pmatrix} $$Dann ist $$\vec{u} \cdot \vec{u}^\perp = x \cdot (-y) + y \cdot x + z \cdot 0 = xy - yx = 0$$
Falls Du Fragen dazu hast, so melde Dich bitte.
Gruß Werner