Ein rotationssymmetrischer Gasdruckbehälter

Question

Aufgabe:Ein rotationssymmetrischer Gasdruckbehälter soll die Form eines Zylinders der Höhe h mit aufgesetzter Halbkugelflächen vom Radius r haben. Sein Volumen V soll 1200dm^3 betragen. Berechnen Sie r und h dersrr, dass die Gesamtoberfläche min. Ist.

1. Stellen Sie die Formeln für die Oberfläche A und das Volumen V des Behälters auf.

2. Zeigen Sie, dass die Oberfläche des Behälter durch die Funktionsgleichung A(r) = 4pi x r^2 - 8pi/3 ×r^2 + 2400/r angegeben werden kann und geben sie einen sinnvollen Definitionsbereich der Funktion an.

3. Bestimmen Sie mithilfe der Differnzialrechnung die Minimslstelle der Funktion. Weisen Sie mittels eines Kriterium nach, dass es sich um eine Minimslstelle handelt.

4. Geben Sie die Maße r und h an.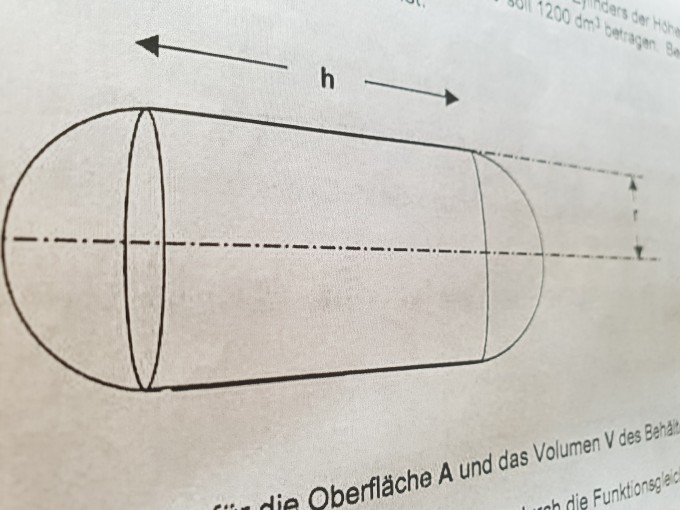

Problem/Ansatz:

Answer 1

V = 4/3·pi·r^3 + pi·r^2·h --> h = V/(pi·r^2) - 4/3·r

O = 4·pi·r^2 + 2·pi·r·h

O = 4·pi·r^2 + 2·pi·r·(V/(pi·r^2) - 4/3·r)

O = 4·pi·r^2/3 + 2·V/r

Das Entspricht jetzt der vorgegebenen Funktion von A wenn sie vereinfacht wird.

O' = 8/3·pi·r - 2·V/r^2 = 0 → r = (3·V/(4·pi))^(1/3)

h = V/(pi·((3·V/(4·pi))^(1/3))^2) - 4/3·(3·V/(4·pi))^(1/3) = 0

Es gilt also

r = (3·V/(4·pi))^(1/3) und h = 0