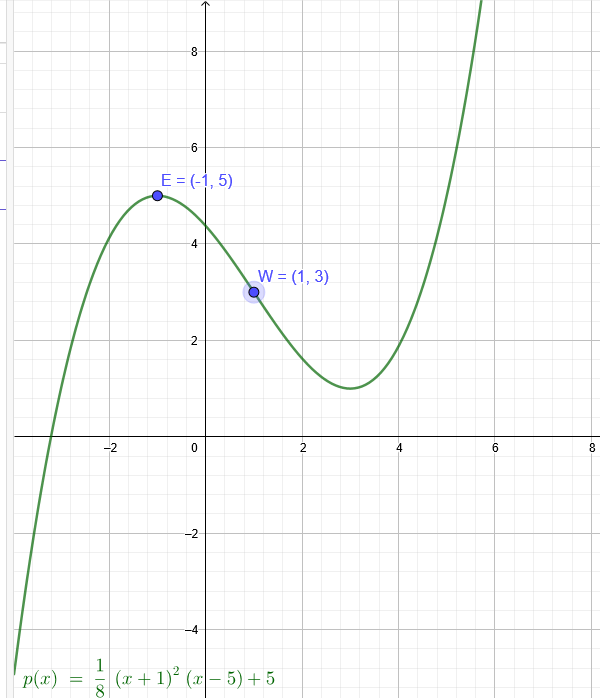
"Der Graph einer ganzrationalen Fkt. 3. Grades hat ein Extrempunkt E(-1|5) und den Wendepunkt W(1|3). Stellen sie die Fkt. auf."
Extrempunkt E(-1|5)→Extrempunkt E´(-1|0)
Wendepunkt W(1|3) →Wendepunkt W´(1|-2)
\(f(x)=a*(x+1)^2*(x-N)\)
\(f(1)=a*(1+1)^2*(1-N)=4a*(1-N)\)
\(4a*(1-N)=-2\)→\(2a*(N-1)=1\)→\(a=\frac{1}{2N-2}\)
\(f(x)=\frac{1}{2N-2}*[(x+1)^2*(x-N)]\)
\(f´(x)=\frac{1}{2N-2}*[(2x+2)*(x-N)+(x+1)^2]\)
\(f´´(x)=\frac{1}{2N-2}*[2*(x-N)+(2x+2)+2*(x+1)]\)
\(f´´(1)=\frac{1}{2N-2}*[2*(1-N)+(2+2)+2*(1+1)]\)
\(f´´(1)=[10-2N]=0\) \([N=5\)→\(a=\frac{1}{8}\)
\(f(x)=\frac{1}{8}*(x+1)^2*(x-5)\)
\(p(x)=\frac{1}{8}*(x+1)^2*(x-5)+5\)