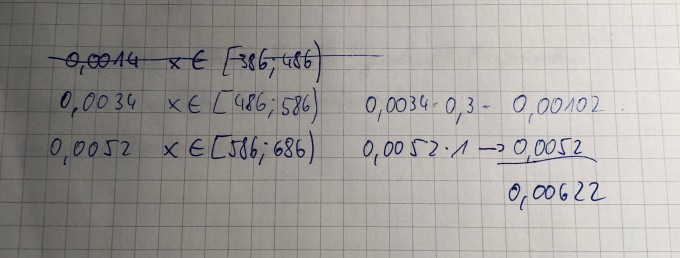Die Zufallsvariable X hat eine stückweise konstante Dichtefunktion F

Question

Aufgabe:

Die Zufallsvariable X hat eine stückweise konstante Dichtefunktion f
Diese ist nachfolgend gegeben durch ihre Abbildungsvorschrift.

Berechnen Sie die Wahrscheinlichkeit P(X>556).

Problem/Ansatz:

Ich habe es mit diesem Lösungsansatz probiert, doch dieser ist leider falsch.

Wäre um jede Hilfe dankbar!

LG Hannah

Comments

wie bist du auf 0,3 und 1 gekommen?

Answer 1

Die Whk. entspricht der Fläche unter der Dichtefunktion auf dem betrachteten Intervall. Bei der stückweise konstanten Funktion entstehen ja nur Rechtecke, so dass man auch ohne Integral auskommt: Bei deiner Rechnung einfach mit 30 und 100, statt mit 0,3 und 1 multiplizieren.

Comments

wie kommt man auf 3 bzw. 30 und auf 1 bzw. 100

---

wie kommt man auf die 30 und 100?

---

Das ist die Länge des Intervalls auf dem die jeweilige Whk. gilt:

Für \(X>556\) haben wir das Intervall von \((556;586)\) der Länge 30 mit einer Whk.dichte von 0,0034 und das Intervall von \([586;686)\) der Länge 100 mit Whk.dichte 0,0052.