Steckbriefaufgabe 4.Grade

Question

Aufgabe:

Bestimme eine ganzrationale Funktion vierten Grades,deren Graph den Wendepunkt O (0/0) mit der x-Achse als Wendetangente und den Tiefpunkt A(-1/-2) hat.

Problem/Ansatz:

Ich habe nur 4 Bedingungen herausgearbeitet :

1. f(-1)=-2

2. f(-1)=0

3. f(0)=0

4. f''(0)=0

nur wiess ich die 5. Bedingung nicht

Answer 1

x-Achse als Wendetangente

heißt:

Die Steigung im Wendepunkt ist gleich der Steigung der x-Achse, also

 f ' ( 0 ) = 0

Answer 2

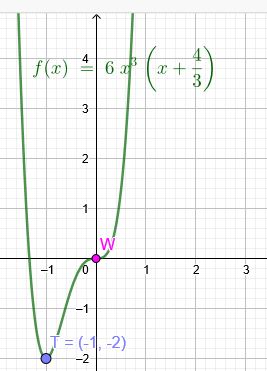
Bestimme eine ganzrationale Funktion vierten Grades, deren Graph den Wendepunkt O\( (0|0) \) mit der x-Achse als Wendetangente und den Tiefpunkt T\((-1|-2)\) hat.

\(f(x)=ax^3(x-N)\) wegen x-Achse als Wendetangente: Dreifachnullstelle.

A\((-1|-2)\):

\(f(-1)=-a(-1-N)\)

\(-a(-1-N)=-2\)

\(a(-1-N)=2\)

\(a=\frac{2}{-N-1}\):

\(f(x)=\frac{2}{-N-1}(x^4-Nx^3)\)

\(f'(x)=\frac{2}{-N-1}(4x^3-3Nx^2)\)

Tiefpunkt T\((-1|...)\):

\(f'(-1)=\frac{2}{-N-1}(-4-3N)\)

\(\frac{2}{-N-1}(-4-3N)=0\)

\(N=-\frac{4}{3}\):

\(a=\frac{2}{\frac{4}{3}-1}=6\):

\(f(x)=6x^3(x+\frac{4}{3})\)