Hallo Julia,
wie in vielen Fällen, so gilt auch hier: mache Dir mal 'ne Skizze. Gegeben ist ein Gerade mit der Steigung \(m\). Zeichen das Steigungsdreieck einfach mal ein. (in der Skizze grün)
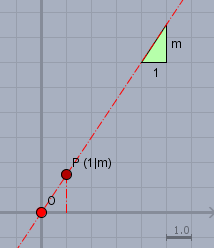
Und dann zeichne den Punkt \(P\) mit den Koordinaten $$P = \begin{pmatrix} 1 \\ m\end{pmatrix}$$Dann siehst Du, dass dieser Punkt auf der Spiegelgeraden (rot) liegt. Er wird also auf sich selbst abgebildet. Genau so, wie es die Abbildung besagt:$$P' = S_m \cdot \begin{pmatrix} 1 \\ m\end{pmatrix} = \begin{pmatrix} 1 \\ m\end{pmatrix} = P$$Natürlich kann man den Wert bzw. die X-Koordinate von \(P\) also \(x=1\) auch in die Geradengleichung einsetzen: \(y(1)=m \cdot 1 = m\). Dann erhält man den Wert für die Y-Koordinate von \(P\). D.h. \(P\) liegt auf der Geraden.
Weiter heißt es:$$S_m \cdot \begin{pmatrix} -m \\ 1\end{pmatrix} = \begin{pmatrix} m \\ -1\end{pmatrix}$$Dazu zeichne ich die folgenden Punkte in die Skizze ein$$Q =\begin{pmatrix} -m \\ 1\end{pmatrix}, \quad Q' = \begin{pmatrix} m \\ -1\end{pmatrix} $$
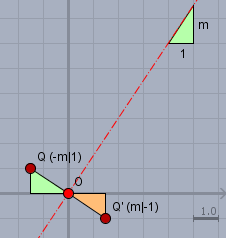
und man kann sehen, dass es sich bei \(Q'\) um eine Spiegelung des Punktes \(Q\) an der Spiegelgeraden handelt. Überlege selber an Hand der kleinen Dreiecke, warum das so sein muss.
Nun soll \(S_m\) bestimmt werden. Dazu haben wir bereits zwei Gleichungen mit \(S_m\). Diese fasse ich jetzt zu einer Matrizengleichung zusammen:$$S_m \cdot \begin{pmatrix} 1 & -m \\ m & 1\end{pmatrix} = \begin{pmatrix} 1 & m \\ m & -1\end{pmatrix}$$Im Grunde haben wir nun eine Gleichung mit einer Unbekannten \(S_m\). ich kenne Deine Vorkenntnisse nicht; frage bitte nach, wenn Du das folgende nicht verstehst. Ich multipliziere rechts mit der Inversen der linken Matrix - macht:$$\begin{aligned}S_m &= \begin{pmatrix} 1 & m \\ m & -1\end{pmatrix} \cdot \begin{pmatrix} 1 & -m \\ m & 1\end{pmatrix}^{-1} \\ &= \begin{pmatrix} 1 & m \\ m & -1\end{pmatrix} \cdot \frac 1{1+m^2} \begin{pmatrix} 1 & m \\ -m & 1\end{pmatrix} \\ &= \frac 1{1+m^2} \begin{pmatrix} 1-m^2 & 2m \\ 2m & m^2-1\end{pmatrix}\end{aligned}$$Für \(m=2\) hieße \(S_2\):$$S_2 = \frac 1{5} \begin{pmatrix} -3 & 4 \\ 4 & 3\end{pmatrix}$$Nun zeichen ein Koordinatensystem und die Gerade \(y=2x\) und führe die Transformation für einige Punkte Deiner Wahl durch. So kannst Du das Ergebnis überprüfen.
Nachtrag: Ist die Ursprungsgerade nicht durch die Steigung \(m\), sondern durch den Winkel \(\alpha\) gegeben, den sie mit der X-Achse einschließt, so lässt sich \(S\) umrechnen:$$\begin{aligned}S_m &= \frac 1{1+m^2} \begin{pmatrix} 1-m^2 & 2m \\ 2m & m^2-1\end{pmatrix} &&|\,m = \tan \alpha \\S_\alpha &= \frac 1{1 + \tan^2\alpha} \begin{pmatrix} 1-\tan^2\alpha & 2\tan \alpha \\ 2\tan\alpha& \tan^2\alpha \end{pmatrix} \\&= \frac{1}{1 + \left(\frac{\sin\alpha}{\cos\alpha}\right)^2}\begin{pmatrix} 1-\left(\frac{\sin\alpha}{\cos\alpha}\right)^2& 2\frac{\sin\alpha}{\cos\alpha}\\2\frac{\sin\alpha}{\cos\alpha}& \left(\frac{\sin\alpha}{\cos\alpha}\right)^2 -1 \end{pmatrix} \\ &= \frac{1}{\cos^2\alpha + \sin^2\alpha} \begin{pmatrix}\cos^2\alpha -\sin^2\alpha & 2\sin\alpha\cos\alpha \\ 2\sin\alpha\cos\alpha & \sin^2\alpha-\cos^2\alpha \end{pmatrix} &&|\,{}^*) \\&= \begin{pmatrix} \cos(2\alpha) & \sin(2\alpha) \\ \sin(2\alpha) & -\cos(2\alpha) \end{pmatrix} \end{aligned} $$\({}^*)\) siehe Doppelwinkelfunktionen.
Gruß Werner
