Differentiale in Polarkoordinaten ohne Jacobi Determinante

Question

Ich versuche das Flächenelement für beliebige Koordinatentransformationen herzuleiten. Dazu findet man allgemein, die Formel mit der Jacobi Determinante, das ist mir bekannt und das kann Ich. Ich versuche jetzt aber das analoge Ergebnis über die einfache Multiplikation der Differentiale zu bekommen und scheitere. Am Beispiel der Polarkoordinaten:

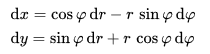
\( dA=dxdy=\cos(\phi)\sin(\phi) dr^2 +rdr d\phi(\cos(\phi)^2-\sin(\phi)^2) -r^2\sin(\phi)\cos(\phi)d\phi^2 \neq rdrd\phi \)

Wo ist der Fehler, was passiert mit den quadratischen Differentialen, wieso sollten die verschwinden?

Answer 1

Hallo

so kannst du mit Differentialen dx, dy nicht umgehen. da du im kartesischen Koordinatensystem rechnest kannst du dir natürlich Miniquadrätchen der Fläche dx*dy vorstellen. wenn du aber andere Koordinaten nimmst werden diese Quadrätchen verzerrt. die Jakobimatrix sagt wie bzw. macht da rückgängig.ich hab mal stark vergrößert dir das Rechteck dx*dy  grün und das Rechteck rdφ*dr aufgemalt, die 2 Flächeninhalte kannst du nicht  mit deiner Rechnung auseinander bestimmen, aber aus der Zeichnung entnehmen wie man in Polarkoordinaten auf dA kommt.

Gruß lul

Comments

Dann war meine Vorstellung doch etwas zu naiv.

Answer 2

man kann das ausrechnen, indem man die Differentiale "multipliziert". Allerdings ist das nicht einfach. Dazu benötigt du wissen über Differentialformen.

Um es mal einfach auszudrücken:

dr  und dphi kommutieren nicht, es gilt drdphi=-dphidr. Beachte also beim aus multiplizieren die Reihenfolge der Terme und wende obige Formel an.

Die Terme mit quadratischer Ordnung in einer Variable fallen weg , weil die zu klein werden.

Siehe auch hier

https://www.matheplanet.com/default3.html?call=viewtopic.php?topic=159951&ref=https%3A%2F%2Fwww.google.com%2F

Comments

Hab mir tatsächlich auch schon überlegt, ob man die quadratischen Terme wegdiskutieren kann. Da Ich Physiker bin, wäre das sogar vermutlich okay gewesen. Ich bin davon ausgegangen das man als Mathematiker das exakt Begründen kann (ohne Näherung). Leider habe Ich überhaupt keine Ahnung von Differentialformen, wusste nichtmal, dass dort ein Kommutator definiert ist.