Integralrechnung brauche Hilfe hab dieses Thema erst heute

Question

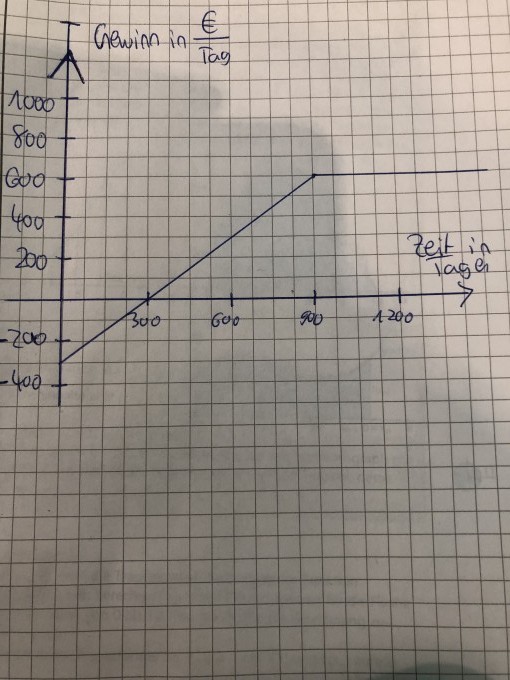
Aufgabe: wie entwickelt sich der gesamtgewinn?

Der Gewinn einer Firma in Abhängigkeit von der Zeit wird die ersten drei Jahre prognostiziert .

a) Wie entwickelt sich der gewinnzufluss ?

Stellen sie markante Punkte heraus

b) Erstellen Sie eine Tabelle für die Entwicklung des gesamtgewinns und zeichnen Sie damit die zugehörige Funktion

Problem/Ansatz:

Comments

Du könntest die Geradengleichung aufstellen für 0<=x<=900

g(x)= m*x+b

m=

Für x>900 gilt: h(x) = 600

Gesamtgewinn = Integral g(x) von 0 bis 900 + Integral h(x) von 900 bis 3*360

Schneller gehts, wenn du die Flächen des Dreiecks und Rechecks addierst.

---

Kannst es für mich ausführlich machen bedanke mich jetzt schon das ihr mir hilft ;)

---

f(x) = m*x+b

2 Punkte aufgreifen z.B. (0/-300) u. (300/0)

m= (0-(-300))/(300-0) = -1

einsetzen:

-300= -1*0+b

b= -300

f(x) = -x-300

∫f(x) = -x^2/2-300 x

∫h(x) = 600x

...

---

warst das mit der a? c;

---

a) (300/0) ist der Breakeven-Punkt

bis x=900 steigt der Gewinn und bleibt dann konstant/stagniert.

b) Verwende die Integrale: Gesamtgewinn = F(x)+H(x), jeweils in den genannten Grenzen.

---

wie bist du da drauf gekommen ∫f(x) = -x2/2-300 x

---

Formel:

x^n wird integriert zu x^(n+1)/(n+1)

Eine Konstante k wird zu k*x

Herleitung:

k= k*1=k*x^0 → k*x^1/1 = k*x

---

hab dieses thema seit 2 tagen und meine lehrerin hat das noch net mal angeschprochen uff

---

∫ also dieses zeichen haben wir noch net besprochen 

---

Das bedeutet "Integral".

Die Flächen bekommt man hier auch ohne Integral, weil sie nicht krumm begrentzt sind. Es ist ein Dreieck und ein Viereck, deren Flächen man leicht berechnen kann mit den Flächenformeln.

Die Flächen sind ein Maß für den Gesamtgewinn.

---

Ich lass mal die Nullen weg. Der Verlust bis 3 ist eine Dreiecksfläche mit den Inhalt 3· 3/2=4,5.Der tiefste Punkt der Parabel ist also (3|4,5).Rechts davon liegt zunächst  (bis x=6) eine kongruente und ebensogroße Dreiecksfläche im Gewinnbereich. Bei x=6 sind Gewinn und Verlust identisch. Hier liegt eine Nullstelle des Gesamtgewinns. Da der tägliche Gewinn danach linear steigt, ist der Gesamtgewinn eine Parabel. Auf ihr liegen die Punkte (0|0), (3|4,5), (6|0). Ab der Stelle x=9 (Punkt (9|27) wächst der Gewinn jeden Tag konstant. Der Gesamtgewinn wächst also linear mit der Steigung 6 (in meiner Skizze falsch).

Answer 1

Zu b) die Gewinnfunktion zu deinemGraphensieht so aus (Einheiten  mal 100)

Comments

Du meinst die Gesamtgewinnfkt. G(x) ist ja schon gegeben.

---

Ja die Frage stand im Buch

---

Der Hinweis galt Roland. :)

---

kannst das auch mit der tabelle lachen also ausführlich weil ich dieses thema seit 2 tagen habe und ich check das net

---

Bedank mich schon mal für die Hilfe

---

Siehe oben. Über meiner Skizze.