Integralrechnung - Was hab ich fehlerhaft berechnet?

Question

Hallo,

ich hoffe, dass mir jemand helfen kann. Es geht um Integralrechnung.

Also ich schreib erstmal meine Lösung auf und dann die vom GTR. Ich hab die Aufgabe gelöst, aber anscheinend falsch, bitte helft mir meinen Fehler zu finden :)

Meine Lösung: (ich hoffe, dass ist verständlich, was ich gemacht habe :))

((1/9*e⁵) - (1/9*e⁰)) + ((1/2*5²+2*5)² - (1/2*0+2*0)²)  = 522,629

GTR:
Integral ⁵ ₀ (1/9*e^x)dx + Integral ⁵ ₀ (x+2)² dx  = 128,046

ich bin mir nicht sicher ob ich mein GTR fotografieren darf, aber ich dachte, dass ich es bestimmt darf, also hier nochmal was ich gerechnet hab :)

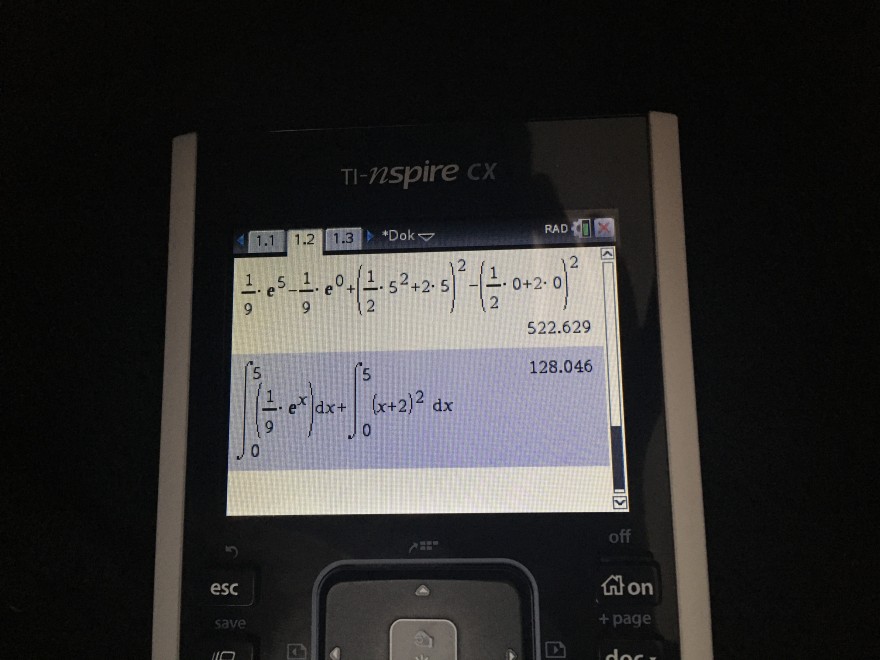
Text erkannt:

TI-VZSbire CX
\begin{tabular}{|l|l|l|l|}
\hline 1.1 & 1.2 & 1.3 & *Dok \\
\hline
\end{tabular}
522.629
\( \int \limits_{0}^{5}\left(\frac{1}{9} \cdot e^{x}\right) d x+\int \limits_{0}^{5}(x+2)^{2} d x \)
off
At on

Text erkannt:

\( \times 2 \) all \( d s u-1 \perp \)

Answer 1

Text erkannt:

\( \int \limits_{0}^{5} \frac{1}{9} e^{x} \cdot d x=\left[\frac{1}{9} e^{x}\right]_{0}^{5}=\frac{1}{9} e^{5}-\frac{1}{9} e^{0}=\frac{1}{9} e^{5}-\frac{1}{9} \approx 16,379 \)
\( \int \limits_{0}^{5}(x+2)^{2} \cdot d x=\int \limits_{0}^{5}\left(x^{2}+4 x+4\right) \cdot d x=\left[\frac{1}{3} x^{3}+\frac{4}{2} x^{2}+4 x\right]_{0}^{5}=\frac{1}{3} \cdot 5^{3}+2 \cdot 5^{2}+4 \cdot 5-0=\frac{335}{3} \)

mfG

Moliets

Comments

Dankeschön, dass hat mein Problem gelöst :)

Answer 2

Ich hab die Aufgabe gelöst,

Interessant wäre zu wissen, WELCHE Aufgabe du gelöst hast.

Geht es um das schnöde Ausrechnen der Summe von zwei Integralen?

Oder sollst du die Größe einer Flächen zwischen Graph und x-Achse berechen?

Oder ein anderer Sachzusammenhang?

PS: Jetzt sehe ich das ganze Elend. Ist dir nicht bewusst, dass (x+2)²=x²+4x+4 ist?

Comments

Ich sollte einfach die Summe von den zwei Integralen ausrechnen, tut mir leid das nicht erwähnt zu haben :)

---

Nein, genau das war mir nicht bewusst, ich Versuch es mal damit zu rechnen, falls ich wieder was nicht verstehe melde ich mich XD Dankeschön!

---

Ich hab es nicht richtig verstanden, weil ich nicht so gut im Stammfunktion bilden bin, aber jemand anders hat es schon erklärt, danke für deine Mühe :)