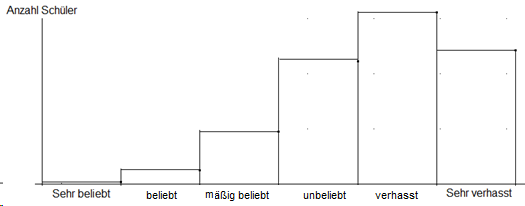
Bei der Befragung einer großen Gruppe von Schülerinnen und Schülern zu ihrer Einstellung zum Mathematikunterricht kommt in der Tendenz etwa das heraus, was die folgende Grafik zeigt:
Der Didaktiker Wolfgang Schlöglmann hat Gründe gesucht, warum so viele Schülerinnen und Schüler das Fach Mathematik hassen. Aus den Antworten greifen wir diejenige eines Oberstufenschülers heraus, die zeigt, dass Schülerinnen in Schüler im Einzelfalle offenbar nur glauben zu wissen, was der Grund ihrer Aversion ist. Der Schüler sagt:
„Das liegt daran, dass man mit der höheren Mathematik im Alltag nicht sehr viel anfangen kann und eigentlich auch nirgends – außer in der Schule – damit konfrontiert wird.“
Der Schüler übersieht, dass viele bereits in der Mittelstufe das Fach Mathematik hassen, obwohl hier überwiegend Alltagsmathematik gelehrt wird. Am Schluss seiner Äußerung widerspricht sich der Schüler teilweise selbst:
„Wie man das ändern könnte, ist theoretisch ganz klar: Den Unterricht interessanter gestalten und realitätsnahe Aufgaben stellen.“
Wo sollen denn die realitätsnahen Aufgaben herkommen, wenn „man mit der höheren Mathematik im Alltag nicht sehr viel anfangen kann“?
Die Vorstellung, mit Anwendungsaufgaben die Motivationsgrundlage für Mathematik im Bewusstsein der Schülerinnen und Schüler zu schaffen, ist unter Didaktikern weit verbreitet. Trotz des offensichtlichen Scheiterns dieses Ansatzes, bleiben viele Didaktiker hartnäckig bei ihrer Überzeugung. Sie nehmen sogar in Kauf, der Praxisbezug der meisten Aufgaben in Lehrbüchern und Klausuren künstlich und realitätsfern konstruiert ist.
Das kann – angesichts gültiger Richtlinien – auch gar nicht anders sein. Denn es geht ja gar nicht darum, den wissenschaftlichen Ansatz des Modellierens zu vermitteln. Das würde auch weit über schulische Möglichkeiten und Lernziele hinausführen. Vielmehr soll grundlegender, schulischer Mathematikstoff geübt werden. Dann wird eben der Verlauf eines Flusses oder einer Straße zu einer kubischen Parabel, was in beiden Fällen zwar nicht der Realität entspricht, aber den klassischen Schulstoff thematisiert.
Der von Schlöglmann befragte, oben zitierte Schüler macht noch den Vorschlag, den Unterricht interessanter zu gestalten, ohne allerdings zu präzisieren, wie das aussehen müsste (abgesehen von seiner widersprüchlichen Forderung nach Realitätsnähe). Die Mathematikdidaktik kommt da, wo sie der Motivationsfrage nachgeht, wie gesagt zu dem Schluss, dass die Motivation der Schülerin oder des Schülers aus der Einsicht gespeist werden müsste, dass die Mathematik durch ihre Anwendungen attraktiv würde. Die Folgen auf Schülerseite und im Aufgabespektrum wurden oben bereits beleuchtet.
Ein Bemühen, diesem Dilemma aus Pseudoanwendungen und ausbleibender Motivation der Schülerinnen und Schüler zu entkommen, ist in der Wissenschaft der Didaktik nicht erkennbar. Der Didaktiker Lynn Arthur Steen (1941-2015) hat diese Situation so beschrieben:
"Mathematikdidaktik bearbeitet ein Feld der Unordnung, ein Feld, auf dem große Hoffnungen auf eine Erziehungswissenschaft von Komplexität und in einem Meer konkurrierender Theorien ertränkt wurden."
Den konkurrierenden Theorien nun eine weitere hinzuzufügen erscheint im ersten Zugriff sinnlos. Das hält erfahrene Schulpraktiker möglicherweise davon ab, einen ganz neuen Ansatz zu finden. Ein solcher Ansatz soll aber im Folgenden versucht werden.
Mathematik – auch höhere Mathematik – kann eine interessante Disziplin sein, wenn man sie Schülerinnen und Schülern
- als grandioses Spiel des Geistes vermittelt,
- ihre Schönheit erkennbar macht und
- erlebbar macht, wie mathematisches Wissen entsteht.
Mathematikunterricht sollte in diesem Sinne möglichst viele Gelegenheiten bieten, etwas zu entdecken.
Schon die Grundschulmathematik bietet zahlreiche Anlässe zum Entdecken. So kann ein Grundschüler entdecken, dass er nur Teile des Einmaleins zu lernen braucht, weil andere Teile daraus herleitbar sind. In diesem Zusammenhang wird implizit das Kommutativgesetz der Multiplikation entdeckt. Beim Übergang zum großen Einmaleins kommt es zwangsläufig zur Anwendung des Distributivgesetzes. Die entdeckten Gesetze werden zwar erst in der Mittelstufe thematisiert aber Wesensmerkmale der Mathematik können schon in der Grundschule geahnt werden.
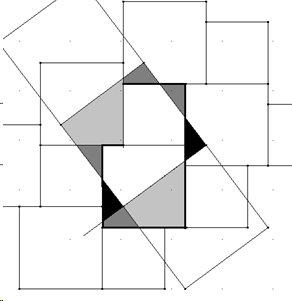
In der Mittelstufe kann beispielsweise der Satz des Pythagoras von Schülerinnen und Schülern entdeckt werden, wenn sie den Auftrag erhalten, die Ebene mit quadratischen Fliesen zweier Größen zu parkettieren und anschließend ein größeres Quadrat in geeigneter Lage darauf gelegt wird, sodass die Parkettlinien dann das große Quadrat in Teilstücke zerschneiden, aus denen sich die kleineren Quadrate des Parketts zusammensetzen lassen.
Und in der Oberstufe können Methoden der Infinitesimalrechnung selbständig entdeckt werden, beim Versuch den Inhalt einer krummlinig begrenzten Fläche mit einer möglichst hohen Genauigkeit zu beschreiben. Die Steigung eines nicht geradlinigen Graphen in einem Punkte kann über die Darstellung eines Wanderweges im Geländequerschnitt eingeführt werden in Verbindung mit der Frage: „Wo hat es der Wanderer besonders leicht oder schwer?“
All diese Beispiele handeln (auch wenn es im letztgenannten Beispiel anders aussieht) nicht von einer Anwendung der Mathematik, sondern machen erlebbar, wie mathematische Wissensbildung geschieht. Wollte man das globale Lernziel des Mathematikunterrichtes in der Vermittlung dieses Erlebnisses sehen, würden vier Dinge erreicht:
- Mathematik wird zum (Erfolgs-)Erlebnis,
- die Tür zur Anwendung von Mathematik wird geöffnet,
- Begriffe und Sätze der Mathematik werden verstanden,
- der Sinn von Gesetzen wird erkannt.
Aber dieses globale Lernziel „erlebbar machen, wie mathematische Wissensbildung geschieht“ setzt voraus, dass der Lehrer oder die Lehrerin eine Idee davon hat, was Mathematik ihrem innersten Wesen nach ist. Charakteristische Wesensmerkmale der Mathematik indessen werden von den meisten Didaktikern für nicht-existent erklärt. Die Mathematik – heißt es – ändere sich ständig und niemand könne eine Definition des Begriffes Mathematik formulieren. Dabei wird außer Acht gelassen, dass jede Änderung genau genommen nur ein Wachstum ist, bei dem zentrale Wesenszüge erhalten bleiben. Unbestritten können sich zwei mathematisch vorgebildete Menschen sehr schnell in der Frage einigen, ob ein Gesprächsthema zur Mathematik gehört oder nicht.
Ein Mathematikunterricht, der erlebbar macht, wie mathematische Wissensbildung geschieht, entfaltet die Mathematik als grandioses Spiel des Geistes und lässt ihre Schönheit immer wieder aufscheinen. In einem solchen Mathematikunterricht geht es immer wieder um eigene Entdeckungen. Diese bewirken Erfolgserlebnisse und sind damit für Neugierige und Hartnäckige motivierend.
Da bliebe für Schülerinnen und Schüler, die überhaupt irgendetwas in der Schule lernen wollen, kein Raum für Hass auf die Mathematik.
Aber leider weigert sich der größte Teil der Mathematikdidaktiker das globale Lernziel von Mathematikunterricht in der Vermittlung des Erlebnisses mathematischer Wissensbildung zu sehen, weil dazu die Frage beantwortet müsste: „Was ist Mathematik?“ Diese Frage wird für ‚falsch gestellt‘ erklärt und durch die Frage ersetzt: “Wozu dient Mathematik?“