Einleitung:
„Ich kann keine Mathe“ hört man oft von Schülerinnen und Schülern. Das ist bereits der Anfang vom Ende jeglichen Mathematik-Könnens. Das Verstehen-Wollen und damit eine zugewandte Einstellung zur Mathematik ist eine grundlegende Voraussetzung, um schließlich Mathematik zu können. Dies gilt natürlich für vieles, was uns nicht in die Wiege gelegt wurde und insbesondere auch für viele Schulfächer.
Über diese Frage der inneren Einstellung hinaus bedarf es noch weiterer Tugenden für das erfolgreiche Betreiben von Mathematik. Dazu gehören insbesondere Phantasie, Kreativität, Neugier und Ausdauer. Aber auch hier liegen keine Alleinstellungsmerkmale der Mathematik.
Die aktuelle Mathematikdidaktik nennt im Bemühen um mathematikspezifische Fähigkeiten und Fertigkeiten 6 sogenannte Kompetenzen, über die Schülerinnen und Schüler verfügen sollten, um letztlich Mathematik zu können:
(K 1) mathematisch argumentieren,
(K 2) Probleme mathematisch lösen,
(K 3) mathematisch modellieren,
(K 4) mathematische Darstellungen verwenden,
(K 5) mit symbolischen, formalen und technischen Elementen der Mathematik umgehen,
(K 6) kommunizieren.
Die Erläuterungen zu diesen Kompetenzen sind geeignet, die im Thema gestellte Frage zu beantworten. Statt aber hier den Text irgendeines Kultusministeriums zu wiederholen, soll ein eigener Ansatz vorgestellt werden, der 6 Kompetenzen anders formuliert:
(M 1) Muster kennen, erkennen, abstrahieren und beschreiben,
(M 2) Präsentationsformen kennen und zwischen ihnen wechseln können,
(M 3) Begriffsvorstellungen altersgemäß entwickeln,
(M4) Regeln, Sätze und Gesetze kennen, anwenden und zum Teil auch herleiten können,
(M 5) Die Sprache der Mathematik verstehen, sprechen, stenographisch aufschreiben und lesen können,
(M 6) Heuristische Strategien und Prinzipien kennen und anwenden können.
Im Folgenden sollen diese Kompetenzen erläutert und beschrieben werden:
Muster kennen, erkennen, abstrahieren und beschreiben
Man kann nur erkennen, was man kennt. Wenn wir chinesische Schriftzeichen nicht kennen, werden wir nichts erkennen, wenn wir sie lesen. Mathematische Schriftzeichen sollten wir kennen. Die Zahlenfolge 1, 8, 27, 64, 125, … sollte demjenigen, der Mathematik treiben möchte, bekannt vorkommen. Eine Beschreibung mit Worten ist dann: „Die Folge der Kubikzahlen“. In mathematischer Stenographie lautet die Beschreibung (n³)nєN.
Auch graphische Darstellungen sollten wir kennen, erkennen und beschreiben können. So sollten wir z.B. Graphen quadratischer und kubischer Parabeln unterscheiden können. Und auch geometrische Muster sollten wir soweit kennen, analysieren und beschreiben können, wie es im Rahmen einer Problemlösung notwendig ist. Schließlich sollte man in der Algebra kürzbaren Termen ihre Faktoren ansehen können (z.B.: (3x²h+3xh²+h³)/h= 3x²+3xh+h²).
Präsentationsformen kennen und zwischen ihnen wechseln können
- Eine Funktion kann z.B. als Gleichung, als Paarmenge oder als Graph dargestellt werden.
- Die Summe der Zahlen von 1 bis 100 kann auf ganz unterschiedliche Arten algebraisch oder geometrisch dargestellt werden. (Mindestens eine Darstellung legt die Summenformel für arithmetische Reihen nahe.)
- Der Satz des Pythagoras ist in einem rechtwinkligen Dreieck mit den Katheten a und b sowie der Hypotenuse c formal mit a²+b²=c² beschrieben. Aber die folgende Skizze legt durch Parallelverschiebung des größten Quadrates eine Fülle von Beweisideen nahe.
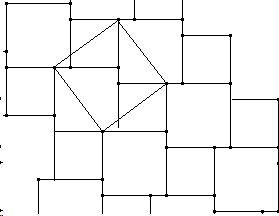
Begriffsvorstellungen altersgemäß entwickeln
Die mathematischen Begriffe werden meistens nicht bei der ersten Begegnung vollständig erfasst. So taucht zum Beispiel der Begriff der Proportionalität bereits beim Kürzen und Erweitern von Brüchen auf, ohne dass die Zahlenpaare (Zähler|Nenner) bereits als proportional beschrieben werden. Im Laufe des Schullebens klingt der Begriff immer wieder an: In den Zusammenlängen „Ähnlichkeit“, “zentrische Streckung“ oder „Dreisatz“ in der Mittelstufe und bei Wachstumsprozessen in der Oberstufe, wenn der Bestand proportional zur Wachstumsgeschwindigkeit ist.
Begriffe werden im Laufe des Schullebens immer mehr vervollständigt. Man merkt sie sich möglichst nicht nur durch Auswendiglernen der Definitionen sondern besser durch geeignete Beispiele und Gegenbeispiele. Das vertiefte Erfassen eines Begriffes ermöglicht schließlich ihre vergegenständlichende Verallgemeinerung, bei der ein Begriff zum Gegenstand eines weiterführenden Gedanken wird. Ist etwa der Zahlbegriff vollständig erfasst, werden weiterführende Gedanken ermöglicht, wie die Verknüpfungen von Zahlen (z.B. +, – , ·, :).
Regeln, Sätze und Gesetze kennen, anwenden und zum Teil auch herleiten können
Auch in der Mathematik kann Auswendiglernen sinnvoll sein. Das gilt zum Beispiel für die Lösungsformel quadratischer Gleichungen, für die Regeln der Bruch- oder Potenzrechnung und für Ableitungsregeln. Aber alles nur auswendig zu wissen, hat zwei Nachteile, die den Zugang zur Mathematik versperren. Vieles bleibt unverstanden und die Menge des auswendig Gelernten wird zu groß, um sich alles merken zu können. Summenformeln für arithmetische und geometrische Reihen etwa können leicht und auf kurzem Wege hergeleitet werden (schon der Grundschüler Gauß konnte das).
Im Rahmen einer Herleitung übt man eine wichtige mathematische Tätigkeit: Das Zurückführen einer Formel oder Regel auf einen einfachen Gedanken. So können z.B. die Flächenformel für das Trapez auf die für das Parallelogramm zurückgeführt werden und diese wiederum auf die einfache Flächenformel für das Rechteck. Die Flächenformel für das Dreieck ist dann auf die für das Parallelogramm zurückführbar und jedes Vieleck ist aus Dreiecken zusammensetzbar.
Die Sprache der Mathematik verstehen, sprechen, stenographisch aufschreiben und lesen können
Die klassischen Kompetenzen
- mathematisch argumentieren,
- mathematisch modellieren und
- mathematisch kommunizieren
erfordern die Beherrschung der mathematischen Sprache in Wort und Schrift einschließlich der zugehörigen stenographischen Zeichen sowie der inhaltlichen Erfassung der Begriffe. Auf diese Weise wird es möglich, immer mehr immer übersichtlicher auszudrücken, was nicht nur die Kommunikation über mathematische Fragstellungen vereinfacht. Gleichzeitig wird die Mathematik als Gesamtgebäude (Turm) übersichtlicher und tragfähiger.
Heuristische Strategien und Prinzipien kennen und anwenden können.
Manche Lehrer und einige Schülerinnen und Schüler glauben, dass man Heuristik nicht lernen oder vermitteln kann. Dazu hat George Polya ein Büchlein verfasst mit dem Titel „Schule des Denkens – Vom Lösen mathematischer Probleme“. Eine der klassischen Kompetenzen heißt „Probleme mathematisch lösen“.
Nach Polya sollte ein Schüler oder eine Schülerin angesichts eines mathematischen Problems zunächst die Frage stellen: „Hast du diese oder eine ähnliche Aufgabe schon einmal gesehen?“ und dann: „Kennst du Lehrsätze, die einen Bezug zur Aufgabe haben könnten?“ Anschließend rät Polya, gesuchte und gegebene Größen zu identifizieren und (oft in einer Skizze) zu benennen. Weiterhin zählt Polya Strategien auf, deren Eignung von Fall zu Fall zu prüfen ist: Hilfslinien oder Hilfsgrößen einführen, vom Ergebnis her rückwärts arbeiten, Teilprobleme abtrennen, auf einen Teil der Gegebenheiten verzichten und Spezialfälle betrachten. Am Schluss soll man die gefundene Lösung noch einmal (möglicherweise auf einem anderen Wege) überprüfen.
Schlussbemerkung
Um Mathematik zu können (aus der Sicht des Schülers) oder Mathematik zu vermitteln (aus der Sicht des Lehrers) muss man die charakteristischen Merkmale der Mathematik kennen und eine Idee davon haben, wie mathematisches Wissen gewonnen wird. Das Erlebnis mathematischen Wissensgewinns kann sehr motivierend sein, sich mit Mathematik zu beschäftigen. Dazu muss aber der Schüler oder die Schülerin in der Lage sein, sich über dieses Erlebnis zu freuen und der Lehrer oder die Lehrerin in der Lage sein, das Erlebnis mathematischen Wissensgewinns zu vermitteln.
Dieser Artikel hat 50 Bonuspunkte erhalten. Schreib auch du einen Artikel.