Lotto 6 aus 49: Wahrscheinlichkeit, dass 2 Gewinnzahlen aufeinander folgen

Question

Aufgabe Wahrscheinlichkeit:

Beim Ziehen der Gewinnzahlen 6 aus 49 ereignete sich, dass MINDESTENS 2 Gewinnzahlen aufeinander folgten. - Wie wahrscheinlich ist dieses Ereignis?

Answer 1

Antwort mit KI erzeugt

Lotto 6 aus 49: Wahrscheinlichkeit, dass 2 Gewinnzahlen aufeinander folgen

Um die Wahrscheinlichkeit zu berechnen, dass bei einer Lottoziehung (6 aus 49) mindestens zwei Gewinnzahlen aufeinander folgen, ist es oft einfacher, zunächst das Gegenereignis zu betrachten: Keine zwei Gewinnzahlen folgen direkt aufeinander. Die Wahrscheinlichkeit dieses Gegenereignisses lässt sich einfacher berechnen, und anschließend kann man die gesuchte Wahrscheinlichkeit als \(1\) minus die Wahrscheinlichkeit des Gegenereignisses finden.

Berechnung des Gegenereignisses (keine aufeinanderfolgenden Zahlen):

Wir haben 49 Zahlen und ziehen 6 davon. Für das Gegenereignis, dass keine der gezogenen Zahlen aufeinander folgt, stellen wir uns vor, dass wir 43 "Nieten" platzieren und dann die 6 Gewinnzahlen zwischen diesen Nieten platzieren, sodass keine zwei Gewinnzahlen direkt nebeneinander stehen. Damit zwischen jeder Gewinnzahl mindestens eine Niete liegt, können wir uns vorstellen, dass wir zuerst die Nieten (43 an der Zahl) platzieren und dann 6 "Plätze" für die Gewinnzahlen zwischen oder am Rand der Nieten wählen.

Diese Anordnung lässt sich berechnen, indem wir die 43 Nieten und die 6 Plätze für die Gewinnzahlen als separate Einheiten betrachten, wodurch wir insgesamt 49 Plätze haben. Da wir jedoch nur die Position der Gewinnzahlen interessiert, welche ohne direkte Nachbarn sein sollen, betrachten wir die 44 möglichen Positionen (einschließlich der Ränder) und wählen 6 aus diesen aus.

Die Anzahl der Möglichkeiten, 6 Positionen ohne direkte Nachbarn aus 44 möglichen zu wählen, ist \( \binom{44}{6} \).

Die Gesamtzahl der möglichen Ziehungen bei einer Lottoziehung (6 aus 49) ist \( \binom{49}{6} \).

Berechnung der Wahrscheinlichkeit für das Gegenereignis:

Die Wahrscheinlichkeit, dass keine zwei Gewinnzahlen direkt aufeinanderfolgen, ist also der Quotient aus den Möglichkeiten, 6 Positionen aus 44 ohne Nachbarn zu wählen, geteilt durch die gesamten Möglichkeiten, 6 aus 49 zu wählen:

\( P(\text{Keine aufeinanderfolgenden Zahlen}) = \frac{\binom{44}{6}}{\binom{49}{6}} \)

Wir setzen die Binomialkoeffizienten ein:

\( P(\text{Keine aufeinanderfolgenden Zahlen}) = \frac{44! / (6! \cdot (44-6)!)}{49! / (6! \cdot (49-6)!)} \)

Vereinfacht:

\( P(\text{Keine aufeinanderfolgenden Zahlen}) = \frac{44!}{6! \cdot 38!} \cdot \frac{6! \cdot 43!}{49!} \)

Weiter vereinfacht sich der Ausdruck zum:

\( P(\text{Keine aufeinanderfolgenden Zahlen}) = \frac{44 \cdot 43 \cdot 42 \cdot 41 \cdot 40 \cdot 39}{49 \cdot 48 \cdot 47 \cdot 46 \cdot 45 \cdot 44} \)

Berechnung der ursprünglichen Wahrscheinlichkeit:

Wir suchen die Wahrscheinlichkeit, dass mindestens zwei Gewinnzahlen aufeinander folgen, also das Komplement des oben berechneten Ereignisses:

\( P(\text{Mindestens zwei aufeinanderfolgende Zahlen}) = 1 - P(\text{Keine aufeinanderfolgenden Zahlen}) \)

Um dies zu veranschaulichen, muss jedes Ergebnis in konkrete Zahlen umgewandelt werden. Doch für den Rahmen dieser Antwort reicht das Verständnis des Lösungswegs, da die eigentliche Berechnung vor allem auf der Verwendung von Binomialkoeffizienten und deren arithmetischen Vereinfachungen beruht.

Durch Einsetzen und Ausrechnen des vorherigen Ergebnisses erhält man die endgültige Wahrscheinlichkeit dafür, dass in einer Ziehung "6 aus 49" mindestens zwei Zahlen direkt aufeinander folgen.

Answer 2

Es gibt 2 Möglichkeiten um auf das Ergebnis zu kommen. Entweder du schaust in welchen Fällen du MINDESTENS 2 aufeinander folgende Gewinnzahlen hast, oder du schaust in welchen Fällen du NICHT mindestens 2 aufeinander folgende Gewinnzahlen bekommst.

Schauen wir uns erstmal die einzelnen Fälle alle an:

Bei 6 Richtigen sind auf jeden Fall 2 Richtige nebeneinander:

Bei 5 Richtigen sind auf jeden Fall 2 Richtige nebeneinander:

Auch bei 4 Richtigen sind immer 2 Richtige nebeneinander:

Bei 3 Richtigen sind, nur wenn auf eine Richtige immer eine Falsche folgt, keine 2 Richtigen nebeneinander:

Bei 2 Richtigen müssen die Richtigen nebeneinander sein, ansonsten hat man keine 2 Richtigen nebeneinander:

Bei 1 Richtige hat man nie 2 Richtige nebeneinander:

Und bei 0 Richtigen hat man auch nie 2 Richtige nebeneinander:

Jetzt geht es ans Rechnen. Ich entscheide mich über die Gegenwahrscheinlichkeit zu gehen.

$$\text{P(0 R.)=}\frac{\begin{pmatrix} 6\\ 0\\ \end{pmatrix}\begin{pmatrix} 43\\ 6\\ \end{pmatrix}}{\begin{pmatrix} 49\\ 6\\\end{pmatrix}}\approx0.43596\\\text{P(1 R.)=}\frac{\begin{pmatrix} 6\\ 1\\ \end{pmatrix}\begin{pmatrix} 43\\ 5\\ \end{pmatrix}}{\begin{pmatrix} 49\\ 6\\\end{pmatrix}}\approx0.41302\\\text{P(2 R.)=}\frac{\begin{pmatrix} 6\\ 2\\ \end{pmatrix}\begin{pmatrix} 43\\ 4\\ \end{pmatrix}}{\begin{pmatrix} 49\\ 6\\\end{pmatrix}}\approx0.13238\\\text{P(3 R.)=}\frac{\begin{pmatrix} 6\\ 3\\ \end{pmatrix}\begin{pmatrix} 43\\ 3\\ \end{pmatrix}}{\begin{pmatrix} 49\\ 6\\\end{pmatrix}}\approx0.01765$$

Jetzt müssen wir noch schauen in wie vielen Fällen, bei 2 und 3 Richtigen, unser gewünschtes Ergebnis zutrifft. Bei 2 Richtigen müssen die 2 Richtigen nebeneinander sein. Wir packen sie vereinfacht mal in eine Box. Dann gibt es ja noch 4 andere Elemente (Zahlen). Insgesamt gibt es also 5 Elemente und dementsprechend 5! Permutationsmöglichkeiten.

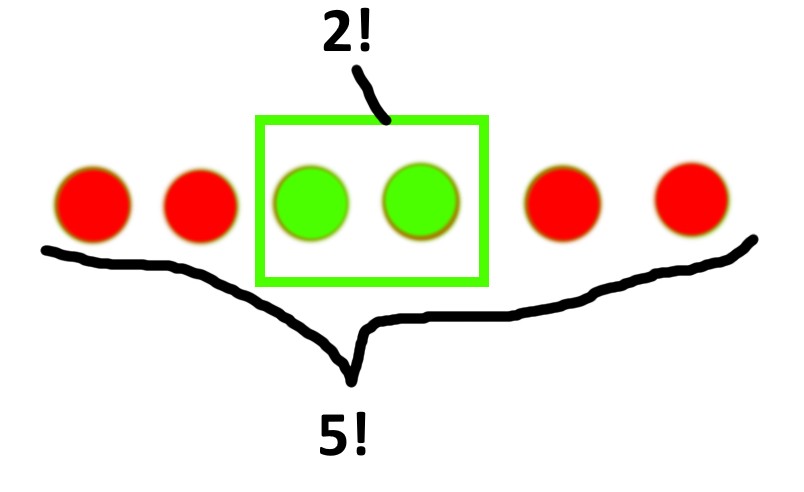
Da die beiden Richtigen noch ihre Position tauschen können, müssen wir hier noch mit 2! multiplizieren. Also 5!*2! = 240. In 240 Fällen sind also 2 Richtige nebeneinander.

Für 6 Zahlen gibt es insgesamt 6! = 720 Permutationen.

Ziehen wir die günstigen Fälle von der gesamten Anzahl ab, kommen wir auf 720-240 = 480 Fälle. Und dies sind 480/720 = 2/3 aller Fälle.

Also müssen wir die Wahrscheinlichkeit von 2 Richtigen mit 2/3 multiplieren, um auf die Wahrscheinlichkeit zu kommen 2 Richtige mit NICHT 2 Richtigen nebeneinander zu ziehen: 0.13238*2/3 = 0.08825.

Und bei 3 Richtigen müssen wir einfach nur schauen, wann es NICHT zutrifft, dass 2 Richtige nebeneinander sind:

Hier haben ja einmal 3! * 3! = 36 Permutationen, wenn die Richtigen und Falschen ihre Position beibehalten sollen. Und da diese Reihe auch mit einer Falschen starten kann, müssen wir noch mit 2 multiplizieren. 36 * 2 = 72

Dies sind 72/720 = 10% aller Fälle. Also müssen wir die Wahrscheinlichkeit von 3 Richtigen mit 1/10 multiplieren um auf die Wahrscheinlichkeit zu kommen 3 Richtige mit NICHT 2 Richtigen nebeneinander zu ziehen: 0.01765*0.1 = 0.001765.

Wenn wir nun alle Fälle, wo wir nicht 2 aufeinander folgende Gewinnzahlen haben, von 1 abziehen kommen wir auf das gesuchte Ergebnis mit: 1 - 0.43596 - 0.41302 - 0.08825 - 0.00177 = 0.061.

A: Die Wahrscheinlichkeit, dass man im Lotto MINDESTENS 2 aufeinander folgende Gewinnzahlen zieht, liegt bei 6.1%.