f(x) = e^{0.5·x}
f'(x) = 0.5·e^{0.5·x}
g(x) = e^{1.5 - 0.25·x}
g'(x) = -0.25·e^{1.5 - 0.25·x}
d) eine ursprungsgerade h berührt den Graphen von f als Tangente. wo liegt der berührpunkt von f und h ? wie lautet die Gleichung von h ?
(f(x) - 0)/(x - 0) = f'(x)
e^{x/2}/x = e^{x/2}/2
x = 2
f(2) = e Berührpunkt
h(x) = f'(2) * (x - 2) + f(2) = e/2·x
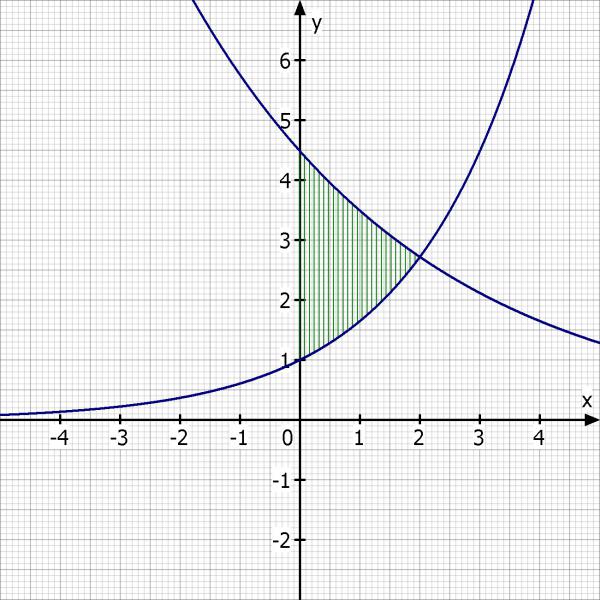
e) wie groß ist die Fläche A , welche von f und g und der y Achse umschlossen wird ?
d(x) = g(x) - f(x) = e^{1.5 - 0.25·x} - e^{0.5·x}
D(x) = - 4·e^{1.5 - 0.25·x} - 2·e^{0.5·x}
D(2) - D(0) = - 6·e - (- 4·e^{3/2} - 2) = 4·e^{3/2} - 6·e + 2 = 3.617 FE
Skizze: