Unter dem Suchbegriff „Falten eines regelmäßigen Fünfecks“ erhält man bei Firefox 400 Ergebnisse. Etwa die Hälfte davon bezieht sich nicht auf Falten oder nicht auf regelmäßige Fünfecke. Die andere Hälfte ist eine bunte Zusammenstellung von Fünfecksfaltungen unterschiedlicher Qualität. Man findet Faltanleitungen,
...die nicht nachvollziehbar sind,
...bei denen ein Winkel oder eine Strecke gemessen werden muss, wodurch die Lösung nicht mehr nur durch Falten entsteht,
...die zu einer Näherungslösung führen und dies zum Teil auch mitteilen, zum Teil aber den Leser im Unklaren darüber lassen,
...die als reine Faltungen zu einem exakten regelmäßigen Fünfeck führen und dies teils auch beweisen, teils einen Beweis schuldig bleiben,
...die als reine Faltungen mit einem unangemessenen Aufwand zu einem exakten regelmäßigen Fünfeck führen,
...die einen Papierstreifen knoten und so trickreich zu einem regelmäßigen Fünfeck gelangen.
Schon Ptolemäus kannte eine Konstruktion, die nur mit Zirkel und Lineal (ohne cm-Einteilung) durchgeführt wurde. Alle sogenannten Grundkonstruktionen mit Zirkel und Lineal lassen sich ohne Zeichengerät auch durch Falten realisieren. Auf diese Weise ist folgende Faltanleitung entstanden:
Faltanleitung
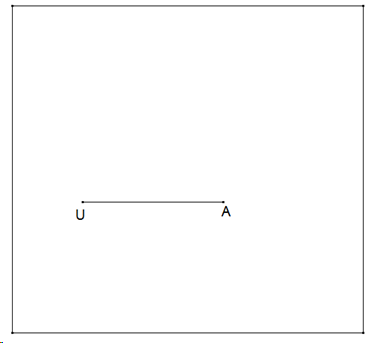
Lege auf einem Blatt Papier die Punkte U und A fest. Die Lage von \( \vec{UA} \) ist zweckmäßiger Weise zu wählen, dass der obere Rand des Blattes mindestens den Abstand 1,5· \( \vec{UA} \) von \( \vec{UA} \) der untere Rand des Blattes mindestens den Abstand 1· \( \vec{UA} \) von ( \( \vec{UA} \) der linke Rand des Blattes mindestens den Abstand 0,5· \( \vec{UA} \)von \( \vec{UA} \), der rechte Rand des Blattes mindestens den Abstand 1· \( \vec{UA} \)von \( \vec{UA} \)hat.
UA liege auf g. Falte eine Senkrechte h zu UA durch A. Beachte, dass aktuelle Faltlinien fett, ältere Faltlinien und der Papierrand nicht fett dargestellt werden.
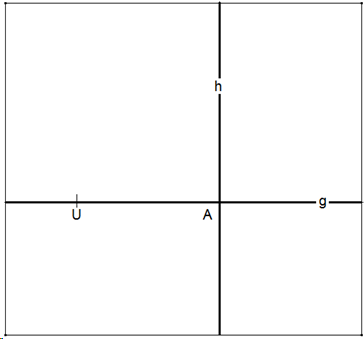
Falte g auf h (Faltlinie durch A) und erhalte den Bildpunkt T von U. Falte U auf A und erhalte E.
Nach dem Öffnen des gefalteten Objektes entsteht die Ansicht links.
Neue Faltlinie ist dann die Mittelsenkrechte von (UA) ̅.
Die Mittelsenkrechte der Strecke UA schneidet g in E.
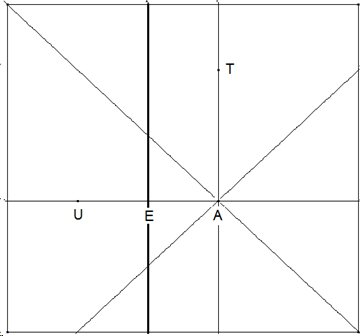
Neue Faltlinie sei die Gerade e=ET.
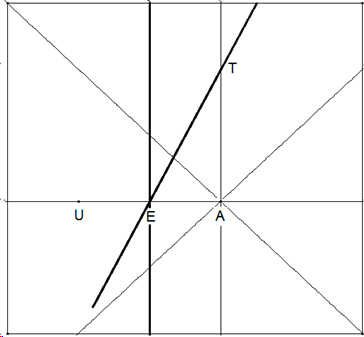
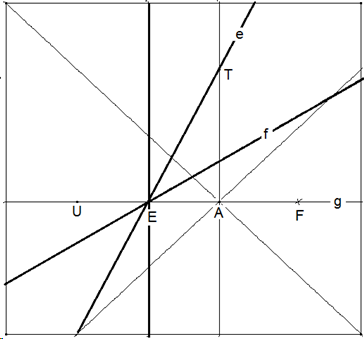
Falte e auf g (Faltlinie f durch E) und erhalte den Bildpunkt F.
Falte h auf e (Faltlinie durch T und erhalte M. Das DreieckMFT ist ein Fünftel des zu faltenden Fünfecks. Die anderen vier Fünftel werden durch wiederholtes Falten des Dreiecks an jeweils einer Seite durch M erreicht.
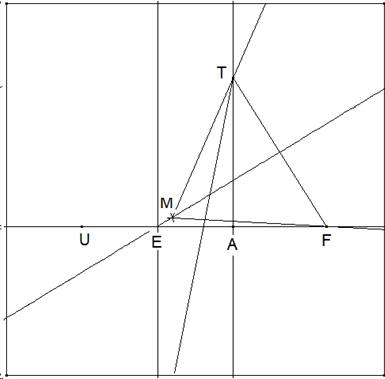
Beweis der Richtigkeit der Konstruktion:
Wir wählen die Länge der Strecke UA als Längeneinheit. Dann haben gemäß Konstruktion auch die Strecken AT und TM diese Länge. Am Schluss der Konstruktion erweist sich M als Mittelpunkt des Umkreises des konstruierten Fünfecks und MF=r als Radius dieses Umkreises.
Laut Formelsammlung gilt für den Umkreisradius r eines regelmäßigen Fünfecks mit der Seitenlänge a: r=a∙√((5+√5)/10). Hier ist r die festgelegte Längeneinheit r=1, die wir einsetzen, um dann nach a aufzulösen. Wir erhalten a=√(10/(5+√2)) und nach rational machen des Nenners des Radikanden: a=√((5-√5)/2). Es geht also nur noch darum zu zeigen, dass TF die Länge a hat.
Nach Pythagoras ist die Länge der Strecke ET = √5/2. Daraus folgt, dass die Länge der Strecke AF=(√5-1)/2 ist und damit nach Pythagoras als Länge der Strecke TF a=√((5-√5)/2).