machen wir uns ein Bild:
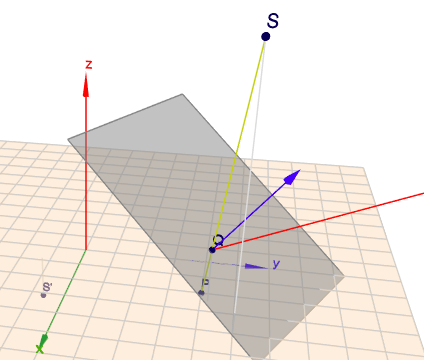
(klick auf das Bild und drehe die Szene mit der Maus)
Der Lichtstrahl von \(S\) aus in Richtung \(P\) ist gelb, seine Reflexion rot gezeichnet. Der blaue Vektor ist der Normalenvektor \(n\) der Ebene \(E: \, x + 2y+ 3z = 16\).
Zur Spiegelung von \(S\) berechnet man zunächst den Abstand \(e\) von \(S\) zur Ebene \(E\). Es ist$$e = \frac 1{|n|} \left( n S - d \right)$$Nach Deinen Angaben ist$$n = \begin{pmatrix} 1\\ 2\\ 3\end{pmatrix} \quad d = 16, \quad S = \begin{pmatrix} 4\\ 5\\ 8\end{pmatrix}$$Der Spiegelpunkt \(S'\) von \(S\) an \(E\) ist dann $$S' = S - 2e \frac n{|n|} = S - \frac 2{n^2}\left(n S - d \right)n = \frac 17 \begin{pmatrix} 6\\ -9\\ -10\end{pmatrix}$$Da \(P\) nicht in \(E\) liegt, muss man noch den Schnittpunkt \(Q\) der Geraden durch \(S\) und \(P\) mit der Ebene \(E\) bestimmen. Dazu setzt man die Geradengleichung$$g: \space x = S + (P-S)t$$ in die Ebenengleichung ein $$E: \space n x = d \\ n \left( S + (P-S)t_Q \right) = d \\ \implies t_Q= \frac{d-nS}{n(P-S)}$$Einsetzen in die Geradengleichung gibt den Schnittpunkt \(Q\)$$Q = S + (P-S) t_Q = \frac 1{14}\begin{pmatrix} 34\\ 59\\ 24\end{pmatrix}$$Die Gerade durch \(S'\) und \(Q\) ist die gesuchte Reflexion des Lichtstrahl.