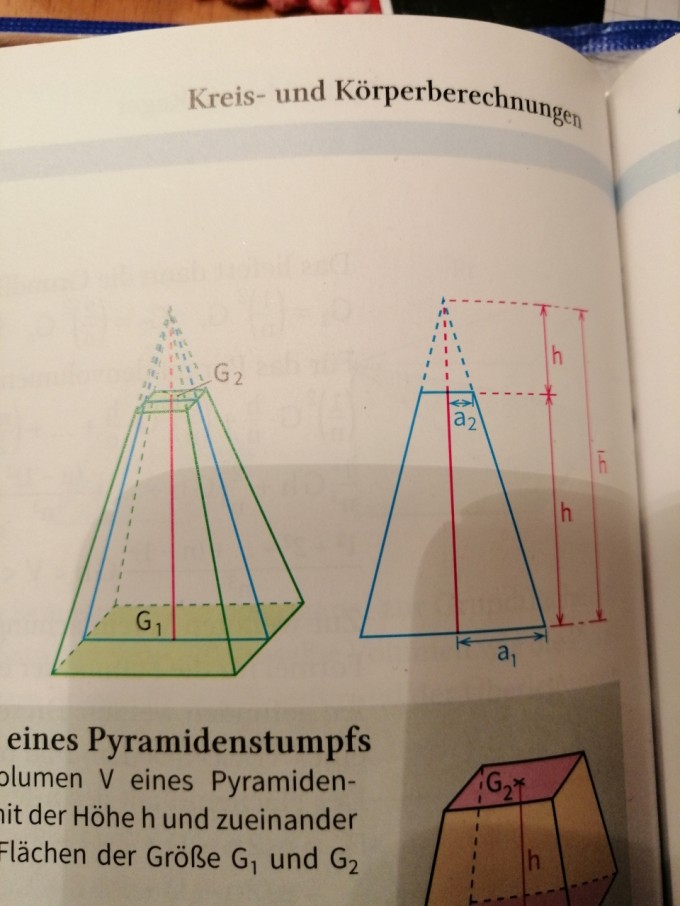
Aufgabe: Die quadratische Pyramide wird 4 cm von der Spitze entfernt parallel zur Grundsläche abgeschnitten. Ferner gilt: G1 = 64 cm² und h = 10 cm
Berechne das Volumen des entstehenden Pyramidenstumpfes, indem du das Volumen der oberen Ergänzungspyramide vom Volumen der ursprünglichen Pyramide abziehst.
Problem/Ansatz: Ich habe einen Lösungsansatz mit Strahlensatz vorliegen. Soweit leuchtet mir der Ansatz auch ein, bis auf einen Sachverhalt:
h*/h = a2/a1
4/14 = a2/4
Laut Zeichnung müsste a1 aber doch nur 2 cm lang sein, oder?
