Aufgabe:
$$ \begin{array}{c}{\text { (a) Beweisen Sie folgende Formel für geometrische Summen: }} \\ {\sum_{i=0}^{n} q^{i}=\frac{q^{n+1}-1}{q-1}, \quad n \in \mathbb{N}, q \neq 1} \\ {\text { Hinweis: Betrachten Sie das Produkt }\left(1+q+q^{2}+\ldots+q^{n}\right)(1-q)}\end{array} $$
$$ \begin{array}{c}{\text { (b) Mit Hilfe von (a) zeigen Sie: Ist q eine Zahl mit }|q|<1, \text { dann gilt }} \\ {\sum_{i=0}^{\infty} q^{i}=\frac{1}{1-q}}\end{array} $$
Problem/Ansatz:
Ich sitze nun schon eine Weile an der Aufgabe b, denn ich habe keine Ahnung wie ich hier rangehen soll.
Hier erst einmal meine Lösung zur Aufgabe a, ich hoffe man sollte es mit der vollständigen Induktion machen, was anderes ist mir nicht eingefallen.
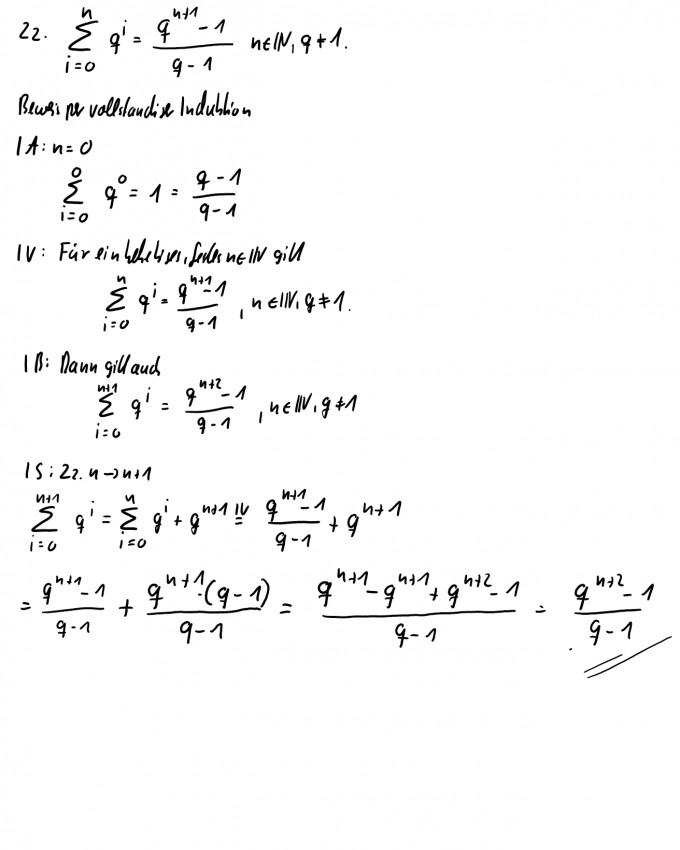
Über einen Anstupser würde ich mich freuen.
LG Anja