a)
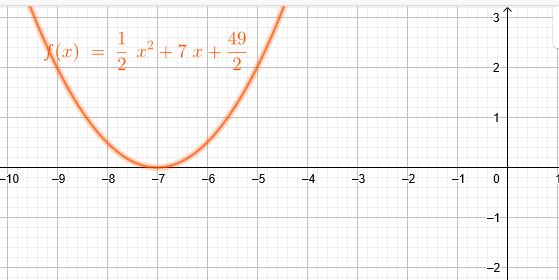
Es existiert dann nur eine Lösung, wenn der Extremwert auf der x-Achse liegt.
\(f(x)=\frac{1}{2} x^2 + 7 x -a\)
\(f'(x)=x + 7\)
\(x + 7=0\)
\(x=-7\) \(f(-7)=\frac{49}{2} -49 -a\)
\(\frac{49}{2} -49 -a=0\)
\(a=- \frac{49}{2} \)
\(f(x)=\frac{1}{2} x^2 + 7 x + \frac{49}{2}\)