Kurvendiskussion: x²*e^{-x}

Question

hey !

könnt ihr mir helfen die extremstellen und wendepunkte auszurechnen?

ich komme auf keine richtigen werte :/

die funktion: f(x)= x²*e^-x

f´(x)= -ehoch-x *(2x+x²)

f``(x)= -ehoch-x *(4x+x²+2)

f`(x)=-e hoch -x *(6x+x²+6)

Answer 1

f(x) = x^2·e^{-x}
f'(x) = e^{-x}·(2·x - x^2)
f''(x) = e^{-x}·(x^2 - 4·x + 2)

Extremstellen f'(x) = 0

2·x - x^2 = 0
x = 2 ∨ x = 0

f(0) = 0
f(2) = 4/e^2 = 0.5413411329

Wendestellen f''(x) = 0

x^2 - 4·x + 2 = 0
x = 2 ± √2
x = 3.414213562 ∨ x = 0.5857864376

f(3.414213562) = 0.3835369905
f(0.5857864376) = 0.1910182260

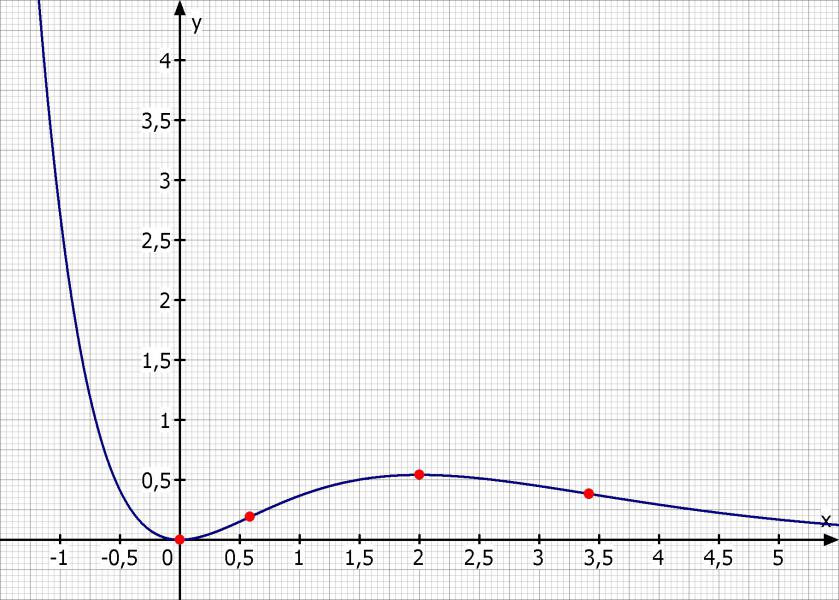
Skizze: