Hallo Lina,
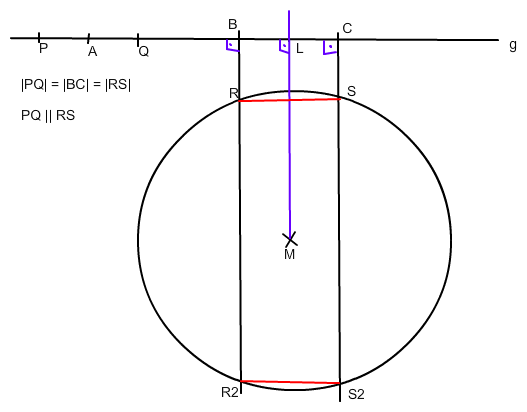
zeichne die Gerade g durch P und Q
Konstruiere die Senkrechte zu g durch M. Diese schneidet g im Punkt L
Halbiere die Strecke PQ (Mittelpunkt A)
Zeichne den Kreis um L mit r = |PA|. Dieser schneidet g in B und C
Konstruiere die Senkrechten zu g durch B und C. Diese schneiden den gegebenen Kreis [erstmalig] in R und S
[ und noch einmal in R2 und S2 ]
Gruß Wolfgang