Integralrechnung: Gerade x=u mit 2<u<10 begrenzt mit den Graphen f(x)=1/4x^2+2 und g(x)=1/2x^2-4x+9 eine Fläche

Question

Probleme bei der Integralrechnung

Aufgabe:

Eine Gerade x=u mit 2<u<10 begrenzt mit den Graphen f(x)=1/4x^2+2 und g(x)=1/2x^2-4x+9 eine Fläche mit dem Inhalt A=40 FE. Berechne den Wert für u.

Problem/Ansatz: Mein Problem ist die generelle Aufgabe, ich weiß absolut nicht wo ich anfangen, geschweige denn wie ich hier etwas berechnen soll.

Freue mich über jegliche Hilfe :)

Comments

Problem: Mein Problem ist die generelle Aufgabe, ich weiß absolut nicht wo ich anfangen, geschweige denn wie ich hier etwas berechnen soll.

Du nimmst deinen GTR und sagst ihm, was er machen soll.

Answer 1

Hallo Peter,
Hier zunächst der Graph

Differenzfunktion bilden

d ( x ) = f - g
d ( x ) = 1/4*x^2+2  - ( 1/2*x^2-4*x+9 )
d ( x ) = - 1/4*x^2 + 4x - 7

Stammfunktion
S ( x ) = -1/12 * x^3 + 2x^2 - 7x

A =[  -1/12 * x^3 + 2x^2 - 7x ] zwischen 2 und u ist gleich 40
A = -1/12 * u^3 + 2u^2 - 7u - ( -1/12 * 2^3 + 2 * 2^2 - 7*2 ) = 40

So. ich geh jetzt erst einmal fernsehen
Vielleicht ist das Newton-Verfahren vonnöten.
x = ca 8.5

Comments

danje danke danke!!!

Answer 2

Hier eine mögliche Vorgehensweise mit einem TI-Nspire CX (kein CAS!):

 

Das sind drei übersichtliche Zeilen.

Comments

Die Schnittstellen von f und g muss man aber vorher überprüfen, oder?

---

Ja. Sonst hat man mit einer Geraden die Fläche noch nicht eindeutig begrenzt.

Schnittpunkt prüfen kannst du mit dem GTR (z.B: Graph ansehen).

---

Das ist richtig.

---

Und hier die andere Lösung:

Answer 3

∫ (2 bis u) ((1/4·x^2 + 2) - (1/2·x^2 - 4·x + 9)) dx = 40 → u = 8.45

~plot~ 1/4*x^2+2;1/2*x^2-4x+9;x=8.45;[[0|10|0|25]] ~plot~

Comments

danje danke danke!!!

Answer 4

Hallo Peter,

g und f haben im Intervall [0 ;10] nur die Schnittstelle x=2, deshalb ergibt sich die Fläche aus einem Integral:

   A(u)  = ₂∫^u (1/4·x^2 + 2 - (1/2·x^2 - 4·x + 9) ) dx  =  - 1/12 · (u^3 - 24·u^2 + 84·u - 80) = 40

Diese Gleichung kann du nicht so einfach nach u auflösen.

Du kannst sie z.B. mit den Cardano- Formeln (aufwändig) oder mit dem Newtonverfahren (Näherungslösung lösen.

Kontrolllösung in [2 ; 10]:   u  ≈  8,445 

Nachtrag:

Newtonverfahren:

Zu lösen ist  h(u) = -1/12 · (u^3 - 24·u^2 + 84·u + 400) = 0  

mit h'(x) = -1/4 · (u^2 - 16·u + 28)

Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man immer bessere Werte mit der Formel

x_neu =  x_alt - f(x_alt) / f ' (x_alt)

Hier bietet sich der mittlere Startwert u=6 in [2 ; 10] an:

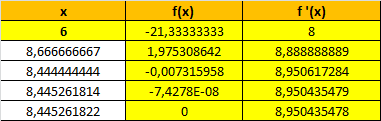
Gruß Wolfgang

Comments

danke danke danke :)