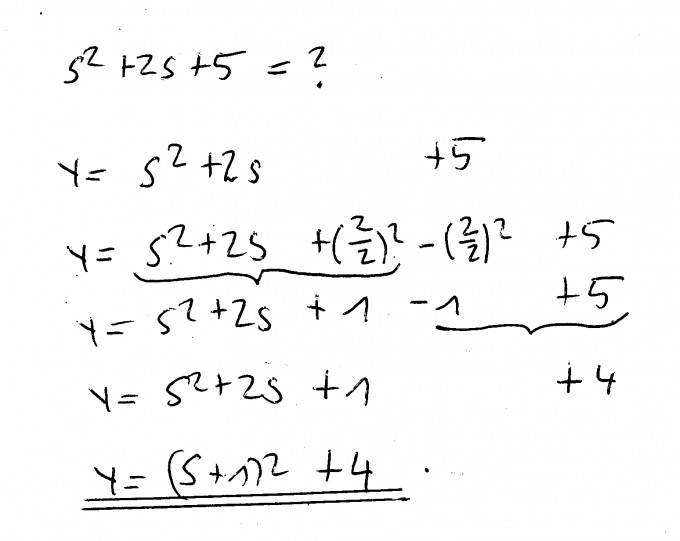Laplace Transformation, Problem bei Rücktransformation

Question

Aufgabe:

y''+2y'+5y=0        y(0)=10   y'(0)=0

Problem/Ansatz:

ich habe für F(s) das Ergebnis (10s+20)/(s^2+2s+5) raus.

unser Prof. hat das ganze weiter mit einer Quadratischen Ergänzung umgeformt, so dass er dann die Rücktransformation durchführen konnte.

Gibt es hier auch eine schönere Lösung? Ich kann doch einfach ganz normal über die Mitternachtsformel die Nullstellen berechnen und mittels Partialbruchzerlegung  zum Ende kommen. Aber das dauert halt ewig. Gibt es vielleicht noch eine einfache schnelle Methode?

Dankeschön!

Comments

https://de.wikipedia.org/wiki/Laplace-Transformation

Laplace ist ein Wort. (korrigiert)

Answer 1

Ich kenne das Ganze auch über die quadratische Ergänzung.

s^2 +2s+5= (s+1)^2+4

-------->

=20/((s+1)^2 +4 )+ 10s/((s+2)^2+4)

Damit geht du in die Laplacetabelle und findest sofort das Ergebnis.

Ich finde , der Zeitaufwand ist nicht so gross.

Du kannst auch direkt aus der  Tabelle " ablésen"

Lösung:

y= 5 e^(-x) (2 cos(2x) +sin(2x))

Comments

Danke dir!

Klar, geht es über die Quadratische Ergänzung schneller. Aber die kann ich nicht :-(

Daher die frage, ob ich es auch klassisch lösen kann mittels Partialbruchzerlegung. DIe dauert natürlich (und vor allem bei mir) wesentlich länger.

Eine andere kurze und leichte Lösung gibt es wohl nicht, oder?

Leider finde ich diese Transformation auch nicht bei mir in der Formelsammlung..

Papula Mathematische Formelsammlung

---

Eine schliessende Klammer fehlt.

Vermutlich

=20/((s+1)^{2} +4 )+ 10s/((s+2)^{2}+4)

?

@quadratische Ergänzung: Das kann man schnell lernen. Man braucht nur die binomischen Formeln genau anzuschauen.

Papula Mathematische Formelsammlung

enthält bestimmt Laplace-Transformationen. Ansonsten z.B: http://siegert.f2.htw-berlin.de/Buero/MB/ltafel.pdf konsultieren.

---

@ Alpenland,

Du mußt es generell immer so rechnen, wie der Prof. das will,

sonst gibt es Punktabzug oder 0 Punkte.

Zu Deinen Fragen:

1.) ob ich es auch klassisch lösen kann mittels Partialbruchzerlegung.

-------->nein, Du kannst hier zwar eine PBZ machen(auf komplexem Wege), aber es gibt dafür keine Tabellen zum Transferieren

2.) Eine andere kurze und leichte Lösung gibt es wohl nicht, oder?

-------->nein
3.) Leider finde ich diese Transformation auch nicht bei mir in der Formelsammlung.Papula Mathematische Formelsammlung

--------->die gibt es da auch nicht.

Das bedeutet, Du wirst nicht umhinkommen, die quadratische Ergänzung zu nutzen , zu lernen.

Besonders gut ist das hier erklärt:

In unserem Fall:

---

Danke dir! Dann werde ich mir das noch mal ansehen..

Wie erkenne ich denn, dass ich das nur lösen kann über eine quadratische ergänzung? gibt es da erkennungszeichen? für mich wäre, wie schon gesagt, die Mitternachtsformel werden der Quadratischen gleichung in Betracht gekommen.

Ich habe in einem Anderen Thema noch eine Frage bzgl Numerischischer Integration gestellt. Speziell die nach Heun. Könntest du mir da noch helfen bitte!?

Vielen Dank!