kann es sein, dass du hier nach dem subtrahieren von 4 das minus vor $$ \frac{e^{-10k}}{e^{-5k}} $$
vergessen hast?
dann solltest du nämlich auf
e^5x = 11/7 kommen.
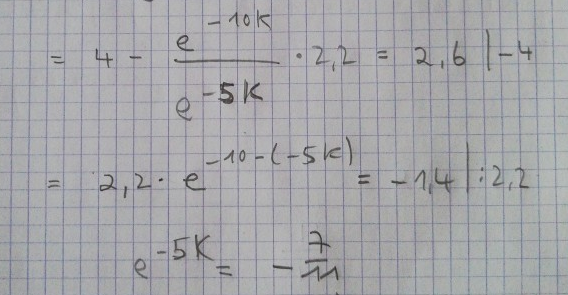
bzw. hier einmal mein Lösungsweg ab hier:
$$ 4 - \frac{e^{-10k}}{e^{-5k}} * \frac{11}{5} = 2.6 $$
$$ 4 - \frac{1}{e^{5x}} * \frac{11}{5} = \frac{13}{5} $$
$$ \frac{11}{5e^{5x}} = \frac{7}{5} $$
$$ 55 = 35e^{5x} $$
$$ e^{5x} = \frac{11}{7} $$
$$ 5x = ln( \frac{11}{7} ) $$
$$ x = \frac{1}{5} * ln( \frac{11}{7}) ≈ 0.0904 $$