Mehrdimensionale Extremstellen

Question

Aufgabe:

Bestimmen Sie die Anzahl der lokalen Minima und lokalen Maxima von f.

f:\( ℝ^{2} \)→ℝ , x(Vektor)→\( e^{x1^{2}+x2^{2}} \) -8\( x1^{2} \) -4\( x2^{4} \)

Zuerst habe ich die Funktion nach x₁ und dann nach x₂abgeleitet.

Um X₁0/X₂0 zu bestimmen, dass ich später benötigen werde um dies in die Formel einzusetzen, um die extremwerte zu bekommen, muss ich ja die Ableitungen fx₁ und fx₂ Nullsetzen. Ich tue dies und da kommt immer nur Müll raus.

Ich habe Probleme diese stationären Punkte zu berechnen. Da können ja mehrere rauskommen wenn ich mich nicht täusche und ich wüsste jetzt nicht welche Punkte ich dann für die späteren Brechnungen verwenden soll.

Ich habe die ganze Zeit versucht X₁/X₂ rauszufinden, 

Ich hab nur rausbekommen

A,B=(±\( \sqrt{ln(8)-1} \),1)

C,D=(\( \sqrt{ln(8)-1} \), ±1)

E,F=(±\( \sqrt{ln(8)} \), 0)

G=(0, 0)

Answer 1

die kritischen Punkte kannst du mit Wolfram kontrollieren:

https://www.wolframalpha.com/input/?i=e%5E(x%5E2%2By%5E2)-8x%5E2%2B4y%5E4+critical+point

Nur E,F und G sind richtig.

Min/Max macht wolfram auch:

https://www.wolframalpha.com/input/?i=e%5E(x%5E2%2By%5E2)-8x%5E2%2B4y%5E4+min

https://www.wolframalpha.com/input/?i=e%5E(x%5E2%2By%5E2)-8x%5E2%2B4y%5E4+max

E,F sind Minima, G ist ein Sattelpunkt

Answer 2

Ist tatsächlich diese Funktion gemeint

f(x, y) = ℯ^(x² + y²) - 8x² - 4y^4

da kommen Arndt Brünner und ich (https://www.geogebra.org/classic/bu3QjrBQ) auf was anderes

muss numerische Lösung verwenden ===> ändern Zeile2 zu: { NSolve(Grad,{x,y}) }  

\(indefinit_{Sattel} = true\)

Comments

Wie meinen sie das?

---

Ich meine, dass sich Georg vertan hat und dass meine Rechnung und der Plot auf einen Sattel hindeutet...

---

Nur einen Sattelpunkt?

---

Hallo Wächter, meine Eingabe

---

Wenn Du genau hinschaust, kannst Du neben dem Sattel TOPs erkennen und auch rechnerisch bestimmen, z.B.

{{x = 0, y = 1.806013755367}}

{{x = 0, y = (-1.806013755367)}}

eingezeichnet hab ich oben nur den Sattelpunkt - weiter

---

Ich bin jetzt komplett verwirrt...

Also muss ich jetzt auf 2 lokale maxima und einen sattelpunkt kommen?

---

Die Funktion ist schwierig zu handeln (deshalb die Frage ob da nicht ein schreibfehler drinsteckt) . Wenn man die z-Achse hoch skaliert, drückt man den zentralen Höcker platt.

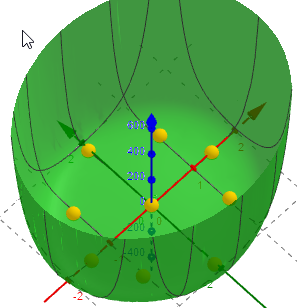
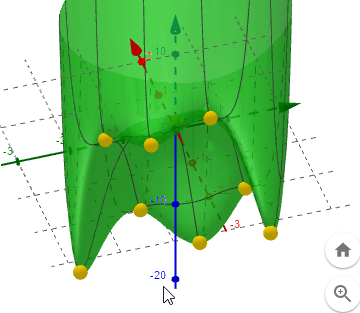
Mit einem Sattel bei (0,0,1) könnten auf dem Höcker auch lokale Max auftreten, die ich nur mit numerischen Verfahren finde und nicht sicher sein kann ob da nicht vielleicht Rundungsfehler mitspielen. Mit ein bisschen rumspielen hab ich mind. 9 kritische Punkte dargestellt.- Ohne Gewähr ;-)

\(\small TOP \, :=  \,  \left\{ \left(0, 0, 1 \right), \left(\sqrt{\ln \left( 8 \right) - 1}, 1, ℯ^{\sqrt{\ln \left( 8 \right) - 1}^{2} + 1} - 8 \; \sqrt{\ln \left( 8 \right) - 1}^{2} - 4 \right), \left(-\sqrt{\ln \left( 8 \right) - 1}, 1, ℯ^{\left(-\sqrt{\ln \left( 8 \right) - 1} \right)^{2} + 1} - 8 \; \left(-\sqrt{\ln \left( 8 \right) - 1} \right)^{2} - 4 \right), \left(\sqrt{\ln \left( 8 \right) - 1}, -1, ℯ^{\sqrt{\ln \left( 8 \right) - 1}^{2} + 1} - 8 \; \sqrt{\ln \left( 8 \right) - 1}^{2} - 4 \right), \left(-\sqrt{\ln \left( 8 \right) - 1}, -1, ℯ^{\left(-\sqrt{\ln \left( 8 \right) - 1} \right)^{2} + 1} - 8 \; \left(-\sqrt{\ln \left( 8 \right) - 1} \right)^{2} - 4 \right), \left(\sqrt{\ln \left( 8 \right)}, 0, ℯ^{\left(\sqrt{\ln \left( 8 \right)}^{2} \right)} - 8 \; \sqrt{\ln \left( 8 \right)}^{2} \right), \left(-\sqrt{\ln \left( 8 \right)}, 0, ℯ^{\left(\left(-\sqrt{\ln \left( 8 \right)} \right)^{2} \right)} - 8 \; \left(-\sqrt{\ln \left( 8 \right)} \right)^{2} \right), \left(0, \frac{181}{100}, ℯ^{\left(\left(\frac{181}{100} \right)^{2} \right)} - 4 \; \left(\frac{181}{100} \right)^{4} \right), \left(0, -\frac{181}{100}, ℯ^{\left(\left(-\frac{181}{100} \right)^{2} \right)} - 4 \; \left(-\frac{181}{100} \right)^{4} \right) \right\} \)

---

Ich bin jetzt von den Antworten total geplättet, weil ich das händisch ausrechnen soll, also mit Gradient und den dann 0 setzen und dann mit der Determinante der Hessematrix und da kommt bei mir halt nur müll raus... :c

Und hab mal bei Wolfram alpha geschaut und das gibt 11 kritische Punkte aus.

---

ja, das kommt hin. mit den 2 numerisch bestimmten in der Nachbarschaft des (0;0;1) Sattels wären es 11. Du brauchst entsprechend der Aufgabe nur die lok. min/max angeben. trotzdem nix, was ich von hand ausrechnen möchte. ich tippe auf druckfehler?

---

Kann schon sein das die ursprünglich eine andere Funktion nehmen wollten, aber auf meinem Aufgabenblatt steht sie genau so. Bei uns in den Aufgaben sind oft Fehler enthalten. Ich frag mich nur wie ich jetzt noch auf die 2 fehlenden punkte kommen soll und warum bei mir bei E und F Minima rauskommen.

---

Ich hab die beiden max

  {x=0, y=-0.380028095195},{x=0, y=0.380028095195}

nur numerisch bei passenden Startwerten erhalten.

Die Rechnung beruht auf dem oben verlinktem ggb-worksheet mit verschiedenen Anpassung zur Lösung der Gradientengleichung. Ich kann es Dir zukommen lassen...

Wenn Du das ^4 zu ^2 änderst, dann sieht das seehr viel übersichtlicher aus?

Answer 3

Bei mir kommt nur 1 Extrempunkt ( Tiefpunkt )
bei ( 0 | 0 ) heraus.