Orthogonalbasis und Projektion

Question

Aufgabe:

Eine Ebene in R^3:

E : 3x1 − 2x2 + x3 = 0

a) Bestimmen Sie eine Orthonormalbasis von E.
b) Bestimmen Sie die Matrixdarstellung P der Orthogonalprojektion auf die Ebene E
bezüglich der kanonischen Basis des R^3

Problem/Ansatz:

Ich weiß nicht wie man die Aufgaben lösen muss/kann. Ich wäre wirklich dankbar, wenn mir jemand die Lösung erklären könnte

Answer 1

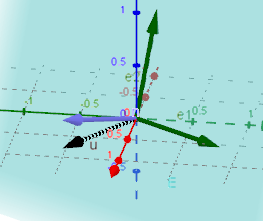
E: n ( x,y,z)=0

E: (3,-2,1) (x,y,z) = 0

Zu a würde ich den Normalenvektor E platt in die z=0 Ebene legen

u=(3,-2,0) und damit die Einheitsvektoren e1, e3 auf die Ebene projezieren.

e1 + t u ∈ E

===> (3,-2,1) (e1 + t u ) =0 ===>   {t = ((-3)) / 13} ===> e1'=(4 / 13, 6 / 13, 0)

e''=e1'/|e1'| = ((2 * sqrt(13) / 13), (3 * sqrt(13) / 13), 0)

analog e3

e3 + t u ∈ E ===> e3''=(((-3) * sqrt(182) / 182), sqrt(182) / 91, sqrt(182) / 14)

e1'' ⊥ e3'' ∈ E

zu b bilde die Einheitsbasis ab

e1 ↦ E : n ((1,0,0) + t n) = 0 ===> {t = ((-3)) / 14} ===> p1=(5 / 14, 3 / 7, ((-3))/ 14)

analog e1,e3

===> \(A \, :=  \, \left(\begin{array}{rrr}\frac{5}{14}&\frac{3}{7}&-\frac{3}{14}\\\frac{3}{7}&\frac{5}{7}&\frac{1}{7}\\-\frac{3}{14}&\frac{1}{7}&\frac{13}{14}\\\end{array}\right)\)