Zeichne die Mittelpunkte aller Grundkreise der vier Zylinder ein und verbinde sie mit Geraden:
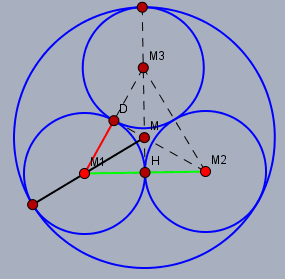
Dann bilden die drei Mittelpunkte der kleinen inneren Zylinder ein gleichseitiges Dreieck mit der Seitenlänge \(a\) (grün). In einem gleichseitigen Dreieck fallen Höhen und Seitenhalbierende zusammen - z.B.: \(HM_3\) - und sind alle gleich lang. Und da das Dreieck gleichseitig ist, ist $$|HM_3| = \frac 12 \sqrt 3 \,a$$Außerdem teilen sich in jedem Dreieck die Seitenhabierenden im Verhältnis \(1\div 2\). Daraus folgt:$$|MM_1| = \frac 23 |HM_3| = \frac 13 \sqrt 3 \, a$$und der Radius \(r\) (schwarz) des großen Kreises ist dann$$r = |MM_1| + |DM_1| = \frac 13 \sqrt 3 \, a + \frac 12 a = (\frac 13 \sqrt 3 + \frac 12) a$$